题目内容
【题目】如图所示,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,AB=1,BC=![]() ,AA1=2,E是侧棱BB1的中点.
,AA1=2,E是侧棱BB1的中点.
(1)求证:A1E⊥平面AED;
(2)求二面角A﹣A1D﹣E的大小.

【答案】(1)见解析,(2) ![]()
【解析】试题分析:
(1)由题意建立空间直角坐标系,求得相关点的坐标后可得![]() ,从而得A1E⊥DA,A1E⊥AE,由线面垂直的判定定理可得结论成立.(2)求出两平面的法向量,根据两个法向量夹角的余弦值可求得二面角的大小.
,从而得A1E⊥DA,A1E⊥AE,由线面垂直的判定定理可得结论成立.(2)求出两平面的法向量,根据两个法向量夹角的余弦值可求得二面角的大小.
试题解析:
(1)证明:∵ 在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,
∴![]() 两两垂直.
两两垂直.
建立如图所示空间直角坐标系![]() .
.
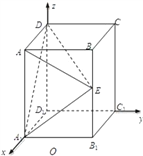
则D(0,0,2),A(![]() ,0,2),E(
,0,2),E(![]() ,1,1),
,1,1),![]() ,C1(0,1,0),
,C1(0,1,0),
∴ ![]() =(
=(![]() ,0,0),
,0,0),![]() =(0,1,﹣1),
=(0,1,﹣1),![]() =(0,1,1),
=(0,1,1),
∴![]() ,
,
∴ A1E⊥DA,A1E⊥AE,
又![]() ,
,
∴ A1E⊥平面AED.
(2)解:设平面A1DE的一个法向量为![]() ,
,
由 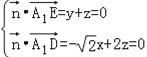 ,得
,得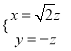 ,
,
令![]() ,得
,得![]() =(
=(![]() ,﹣1,1).
,﹣1,1).
∵![]() ⊥平面AA1D,
⊥平面AA1D,
∴平面AA1D的一个法向量为![]() =(0,1,0),
=(0,1,0),
∴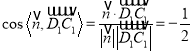 ,
,
由图形得二面角A﹣A1D﹣E是锐角,
∴二面角A﹣A1D﹣E的大小为![]() .
.

练习册系列答案
相关题目
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图(如图),解答下列问题:
分组 | 频数 | 频率 |
[50,60) | 4 | 0.08 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | 0.20 |
[80,90) | 16 | 0.32 |
[90,100] | ||
合计 |
(1)填充频率分布表中的空格;
(2)不具体计算频率/组距,补全频率分布直方图.