题目内容
【题目】如图,在直角坐标![]() 中,设椭圆
中,设椭圆![]()
![]() 的左右两个焦点分别为
的左右两个焦点分别为![]() ,过右焦点
,过右焦点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与椭圆
与椭圆![]() 相交,其中一个交点为
相交,其中一个交点为![]() .
.
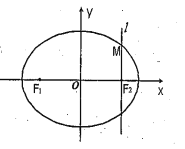
(1)求椭圆![]() 的方程;
的方程;
(2>已知![]() 经过点
经过点![]() 且斜率为
且斜率为![]() 直线
直线![]() 与椭圆
与椭圆![]() 有两个不同的
有两个不同的![]() 和
和![]() 交点,请问是否存在常数
交点,请问是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出
共线?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1) ![]() (2)不存在常数
(2)不存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线.
共线.
【解析】试题分析:(1)由过右焦点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与椭圆
与椭圆![]() 相交,其中一个交点为
相交,其中一个交点为![]() ,可得
,可得![]() ,再根据椭圆的定义以及勾股定理列方程求得
,再根据椭圆的定义以及勾股定理列方程求得![]() 从而得
从而得![]() ,进而可得椭圆的标准方程;(2)直线
,进而可得椭圆的标准方程;(2)直线![]() 的方程为
的方程为![]() 与椭圆方程联立,可得
与椭圆方程联立,可得![]() ,由
,由![]() ,解得
,解得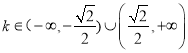 ,
, ![]() 与
与![]() 共线等价于
共线等价于![]() ,根据韦达定理以及向量的坐标运算法则可得关于
,根据韦达定理以及向量的坐标运算法则可得关于![]() 的方程,解得
的方程,解得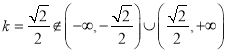 ,从而可得结论.
,从而可得结论.
试题解析:(1)由椭圆定义可知![]() .
.
由题意![]() ,
,![]() .
.
又由![]() △
△![]() 可知
可知 ![]() ,
,![]() ,
,![]() ,
,
又![]() ,得
,得![]() .
.
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
代入椭圆方程,得![]() .
.
整理,得![]() ①
①
因为直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() 等价于
等价于![]() ,
,
解得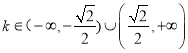 .
.
设![]() ,则
,则![]() =
=![]() ,
,
由①得![]() ②
②
又![]() ③
③
因为![]() , 所以
, 所以![]() .
.
所以![]() 与
与![]() 共线等价于
共线等价于![]() .
.
将②③代入上式,解得![]() .
.
因为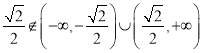
所以不存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线.
共线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目