题目内容
【题目】如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.
(Ⅰ)求圆C的方程;
(Ⅱ)过点M任作一条直线与椭圆 ![]() 相交于两点A、B,连接AN、BN,求证:∠ANM=∠BNM.
相交于两点A、B,连接AN、BN,求证:∠ANM=∠BNM.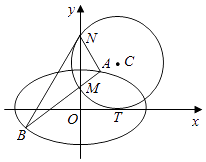
【答案】解:(Ⅰ)设圆C的半径为r(r>0),依题意,圆心坐标为(2,r). ∵|MN|=3,∴ ![]() ,解得
,解得 ![]() ,
,
故圆C的方程为 ![]() .
.
(Ⅱ)把x=0代入方程 ![]() ,解得y=1或y=4,
,解得y=1或y=4,
即点M(0,1),N(0,4).
①当AB⊥y轴时,由椭圆的对称性可知∠ANM=∠BNM.
②当AB与y轴不垂直时,可设直线AB的方程为y=kx+1.
联立方程 ![]() ,消去y得,(1+2k2)x2+4kx﹣6=0.
,消去y得,(1+2k2)x2+4kx﹣6=0.
设直线AB交椭圆Γ于A(x1 , y1)、B(x2 , y2)两点,
则 ![]() ,
, ![]() .
.
∴ ![]() =0,
=0,
∴∠ANM=∠BNM.
综上所述,∠ANM=∠BNM.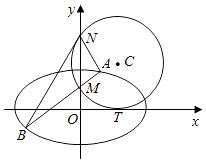
【解析】(Ⅰ)设圆C的半径为r(r>0),依题意,圆心坐标为(2,r),根据|MN|=3,利用弦长公式求得r的值,可得圆C的方程.(Ⅱ)把x=0代入圆C的方程,求得M、N的坐标,当AB⊥y轴时,由椭圆的对称性可知∠ANM=∠BNM,当AB与y轴不垂直时,可设直线AB的方程为y=kx+1,代入椭圆的方程,利用韦达定理求得KAB+KBN=0,可得∠ANM=∠BNM.
【考点精析】解答此题的关键在于理解圆的标准方程的相关知识,掌握圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

