Question

【题目】在平面直角坐标系中，直线l的参数方程为为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ＝asinθ（a≠0）.

（1）求圆C的直角坐标方程与直线l的普通方程；

（2）设直线l截圆C的弦长是半径长的倍，求a的值.

Answer 1

【答案】（1）圆C的方程为；直线l的方程为；

（2）或.

【解析】

（1）结合极坐标与直角坐标的互化公式，即可求得圆C的直角坐标方程，消去参数，即可求得直线l的普通方程；

（2）由（1）中直线和圆的方程，结合直线与圆的位置关系，利用题设条件和点到直线的距离公式，列出方程，即可求解.

（1）由题意，圆C的极坐标方程为，即，

又由，所以，即圆C的直角坐标方程为，

由直线l的参数方程为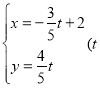为参数），可得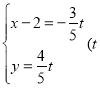为参数），

两式相除，化简得直线l的普通方程为.

（2）由（1）得圆C：，直线l：，

因为直线l截圆C的弦长等于圆C的半径长的倍，

所以圆心C到直线l的距离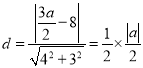，解得或.