题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,设
,设![]() ,证明:
,证明:![]() ,
,![]() ,使
,使![]() .
.
【答案】(1)见解析;(2)证明见解析.
【解析】
(1)![]() ,分
,分![]() ,
,![]() ,
,![]() ,
,![]() 四种情况讨论即可;
四种情况讨论即可;
(2)问题转化为![]() ,利用导数找到
,利用导数找到![]() 与
与![]() 即可证明.
即可证明.
(1)![]() .
.
①当![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,所以,
,所以,
![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
②当![]() 时,
时,![]() ,
,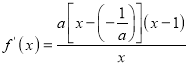 .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,所以,
,所以,
![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
在![]() 上是减函数.
上是减函数.
③当![]() 时,
时,![]() ,
,
则![]() 在
在![]() 上是减函数.
上是减函数.
④当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以,![]() 在
在![]() 上是减函数,
上是减函数,
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(2)由题意,得![]() .
.
由(1)知,当![]() ,
,![]() 时,
时,![]() ,
,
![]() .
.
令![]() ,
,![]() ,
,![]()
故![]() 在
在![]() 上是减函数,有
上是减函数,有![]() ,
,
所以![]() ,从而
,从而![]() .
.
![]() ,
,![]() ,
,
则![]() ,
,
令![]() ,显然
,显然![]() 在
在![]() 上是增函数,
上是增函数,
且![]() ,
,![]() ,
,
所以存在![]() 使
使![]() ,
,
且![]() 在
在![]() 上是减函数,
上是减函数,
在![]() 上是增函数,
上是增函数,
![]() ,
,
所以![]() ,
,
所以![]() ,命题成立.
,命题成立.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案【题目】某公司甲、乙两个班组分别试生产同一种规格的产品,已知此种产品的质量指标检测分数不小于70时,该产品为合格品,否则为次品,现随机抽取两个班组生产的此种产品各100件进行检测,其结果如下表:
质量指标检测分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
甲班组生产的产品件数 | 7 | 18 | 40 | 29 | 6 |
乙班组生产的产品件数 | 8 | 12 | 40 | 32 | 8 |
(1)根据表中数据,估计甲、乙两个班组生产该种产品各自的不合格率;
(2)根据以上数据,完成下面的2×2列联表,并判断是否有95%的把握认为该种产品的质量与生产产品的班组有关?
甲班组 | 乙班组 | 合计 | |
合格品 | |||
次品 | |||
合计 |
(3)若按合格与不合格比例,从甲班组生产的产品中抽取4件产品,从乙班组生产的产品中抽取5件产品,记事件A:从上面4件甲班组生产的产品中随机抽取2件,且都是合格品;事件B:从上面5件乙班组生产的产品中随机抽取2件,一件是合格品,一件是次品,试估计这两个事件哪一种情况发生的可能性大.
附:![]()
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |