题目内容
证明函数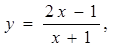 
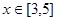是增函数，并求函数的最大值和最小值。
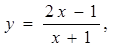
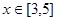是增函数，并求函数的最大值和最小值。．证明：见解析，当x=3时，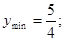
当x=5时，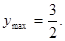
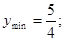当x=5时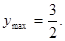，本试题主要是考查了函数的 单调性以及函数的最值的求解。
先利用函数的定义法，设出变量，然后代入解析式，作差，变形定号，最后下结论。得到函数的单调性的证明，进而得到最值。
证明：设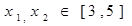
且
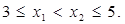
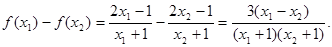
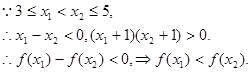
是增函数。
当x=3时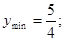， 当x=5时，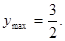
先利用函数的定义法，设出变量，然后代入解析式，作差，变形定号，最后下结论。得到函数的单调性的证明，进而得到最值。
证明：设
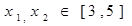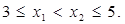
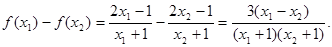
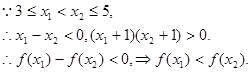
且是增函数。当x=3时，
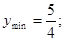当x=5时，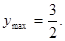
练习册系列答案
相关题目
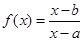在区间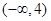
上是增函数，则有（ ）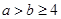
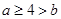
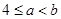
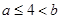
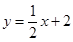，则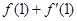
= .
上是减函数，则实数a的取值范围是 ( )
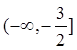
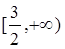
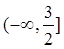
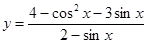的最大值是（ ）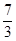
，
，
，
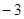
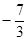
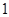
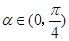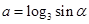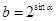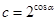，那么a，b，c的大小关系是( )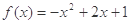
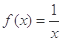
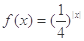
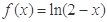
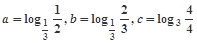，则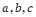
大小关系是__ _
__