题目内容
16.设x∈(0,$\frac{π}{2}$),lgsin2x-lgsinx=-1,则cosx等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{20}$ | D. | $\frac{1}{40}$ |
分析 根据对数函数的运算性质和二倍角的正弦公式得到lg$\frac{2sinxcosx}{sinx}$=lg2cosx=-1,则2cosx=$\frac{1}{10}$,由此可以解得cosx的值.
解答 解:∵x∈(0,$\frac{π}{2}$),lgsin2x-lgsinx=-1,
∴lgsin2x-lgsinx=lg$\frac{sin2x}{sinx}$=lg$\frac{2sinxcosx}{sinx}$=lg2cosx=-1,
则2cosx=$\frac{1}{10}$,
解得cosx=$\frac{1}{20}$.
故选:C.
点评 本题考查了二倍角的正弦,对数的运算性质,属于基础题,牢记sin2α=2sinα•cosα是解题的突破口.

练习册系列答案
相关题目
6.已知数列{an}满足a1=3,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$,则a2012=( )
| A. | 2 | B. | -3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
7.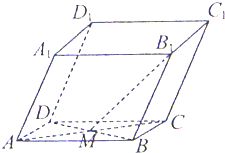 在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
 在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )| A. | -$\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | B. | -$\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ |
11.设α=2014°,则下列判断正确的是( )
| A. | sinα>0,cosα>0,tanα>0 | B. | sinα>0,cosα<0,tanα<0 | ||
| C. | sinα<0,cosα<0,tanα>0 | D. | sinα<0,cosα>0,tanα<0 |
8.若将如图的展开图还原成成正方体,则∠ABC的度数为( )
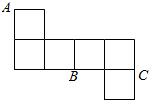

| A. | 120° | B. | 90° | C. | 60° | D. | 45° |