题目内容
16.下列命题中,真命题是( )| A. | 存在x∈R,使ex≤0 | |
| B. | 对任意x∈R,2x>x2 | |
| C. | a+b=0的充要条件是$\frac{a}{b}=-1$ | |
| D. | A,B是△ABC的内角,A>B是sinA>sinB的充要条件 |
分析 由指数函数的值域判断A;举例说明B、C错误;在△ABC的内角,结合正弦定理可证A>B是sinA>sinB的充要条件.
解答 解:由指数函数的值域为(0,+∞)说明A错误;
当x=2时,2x=x2,B错误;
当a=b=0时,a+b=0,此时$\frac{a}{b}=-1$不成立,C错误;
A,B是△ABC的内角,若A>B,则a>b,由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,得sinA>sinB.
若sinA>sinB,由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,得a>b,则A>B,
∴A>B是sinA>sinB的充要条件,D正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了充分条件和必要条件的判断方法,利用正弦定理确定边角关系,是分析选项D的关键,属中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
1.设复数z的共扼复数为$\overline{z}$,若z+$\overline{z}$=4,z•$\overline{z}$=5,且复数z在复平面上表示的点在第四象限,则z=( )
| A. | 2一$\sqrt{21}$i | B. | $\sqrt{21}$一2i | C. | 1一2i | D. | 2一i |
8.有下列关系:(1)人的年龄与他(她)体内脂肪含量之间的关系;(2)曲线上的点与该点的坐标之间的关系;(3)红橙的产量与气候之间的关系;(4)学生与他(她)的学号之间的关系.其中有相关关系的是( )
| A. | (1)、(2) | B. | (1)、(3) | C. | (1)、(4) | D. | (3)、(4) |
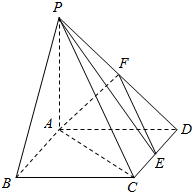 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,且PA=AD,点F是棱PD的中点,点E在棱CD上移动.求证:PE⊥AF.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,且PA=AD,点F是棱PD的中点,点E在棱CD上移动.求证:PE⊥AF.