题目内容
6．
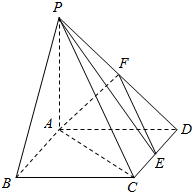如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，且PA=AD，点F是棱PD的中点，点E在棱CD上移动．求证：PE⊥AF．
分析 要证PE⊥AF，因为PE?面PCD，可证AF⊥面PCD，由已知底面ABCD是正方形，PA⊥平面ABCD，易得AF⊥CD，再由PA=AD，点F是棱PD的中点得到AF⊥PD，则问题得证．
解答 证明：∵PA⊥平面ABCD，CD?平面ABCD
又ABCD是矩形，∴CD⊥AD，
∵PA∩AD=A，∴CD⊥平面PAD．
∵AF?平面PAD，∴AF⊥CD．
∵PA=AD，点F是PD的中点，∴AF⊥PD．
又CD∩PD=D，∴AF⊥平面PDC．
∵PE?平面PDC，∴PE⊥AF．
点评 本题考查了由线面垂直得线线垂直，考查了学生的空间想象能力和思维能力，是中档题．
练习册系列答案
相关题目
16．下列命题中，真命题是（ ）
| A． | 存在x∈R，使ex≤0 | |
| B． | 对任意x∈R，2x＞x2 | |
| C． | a+b=0的充要条件是$\frac{a}{b}=-1$ | |
| D． | A，B是△ABC的内角，A＞B是sinA＞sinB的充要条件 |
15．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+3x（x≥0）}\\{g（x）（x＜0）}\end{array}\right.$为奇函数，则f（g（-1））=（ ）
| A． | -28 | B． | -8 | C． | -4 | D． | 4 |
16．已知△ABC的两边长分别为2，3，这两边的夹角的余弦值为$\frac{1}{3}$，则△ABC的外接圆的直径为（ ）
| A． | $\frac{9\sqrt{2}}{2}$ | B． | $\frac{9\sqrt{2}}{4}$ | C． | $\frac{9\sqrt{2}}{6}$ | D． | 8$\sqrt{2}$ |