Question

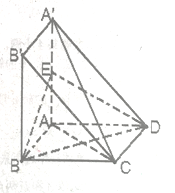
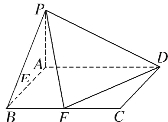
【题目】已知在四棱锥中，底面是矩形，且，，平面，、分别是线段、的中点．

（1）证明：

（2）在线段上是否存在点，使得∥平面，若存在，确定点的位置；若不存在，说明理由．

（3）若与平面所成的角为，求二面角的余弦值

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）

【解析】

试题分析：（1）利用已知的线面垂直关系建立空间直角坐标系，准确写出相关点的坐标，从而将几何证明转化为向量运算．其中灵活建系是解题的关键．（2）证明证线线垂直，只需要证明直线的方向向量垂直；（3）把向量夹角的余弦值转化为两平面法向量夹角的余弦值;（4）空间向量将空间位置关系转化为向量运算，应用的核心是要充分认识形体特征，建立恰当的坐标系，实施几何问题代数化．同时注意两点：一是正确写出点、向量的坐标，准确运算；二是空间位置关系中判定定理与性质定理条件要完备．

试题解析：解法一：（1）∵ 平面，，，，建立如图所示的空间直角坐标系，则． 2分

不妨令∵，∴，

即． 4分

（2）设平面的法向量为，由，得，令，

得：．∴． 6分

设点坐标为，，则，要使∥平面，只需，即，得，从而满足的点即为所求． 8分

（3）∵，∴是平面的法向量，易得， 9分

又∵平面，∴是与平面所成的角，

得，，平面的法向量为 10分

∴，

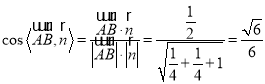故所求二面角的余弦值为． 12分

解法二：（1）证明：连接，则，，

又，∴ ，∴ 2分

又，∴ ，又，

∴ 4分

（2）过点作交于点，则∥平面，且有 5分

再过点作∥交于点，则∥平面且，∴ 平面∥平面 7分 ∴ ∥平面．从而满足的点即为所求． 8分

（3）∵平面，∴是与平面所成的角，且．

∴ 9分

取的中点，则，平面，

在平面中，过作，连接，则，

则即为二面角的平面角 10分

∵∽，∴ ，∵，且

∴ ，，∴ 12分