ЬтФПФкШн
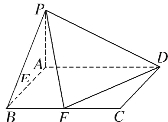
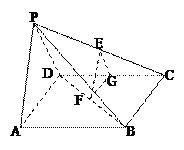
ЁОЬтФПЁПвбжЊЖЏЕу P гыЖЈЕу![]() ЕФОрРыКЭЫќЕНЖЈжБЯп x 4 ЕФОрРыЕФБШЪЧ1: 2 ЃЌМЧЖЏЕу P ЕФЙьМЃЮЊЧњЯп EЃЎ
ЕФОрРыКЭЫќЕНЖЈжБЯп x 4 ЕФОрРыЕФБШЪЧ1: 2 ЃЌМЧЖЏЕу P ЕФЙьМЃЮЊЧњЯп EЃЎ
ЃЈ1ЃЉЧѓЧњЯп E ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩш A ЪЧЧњЯп E ЩЯЕФвЛИіЕуЃЌжБЯп AF НЛЧњЯп E гкСэвЛЕу BЃЌвд AB ЮЊБпзївЛИіЦНааЫФБпаЮЃЌЖЅЕу AЁЂBЁЂCЁЂD ЖМдкЙьМЃ E ЩЯЃЌХаЖЯЦНааЫФБпаЮ ABCD ФмЗёЮЊСтаЮЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЦНааЫФБпаЮ ABCD ЕФУцЛ§ШЁЕНзюДѓжЕЪБЃЌХаЖЯЫќЕФаЮзДЃЌВЂЧѓГіЦфзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉВЛФмЪЧСтаЮЃЛЃЈ3ЃЉОиаЮ
ЃЛЃЈ2ЃЉВЛФмЪЧСтаЮЃЛЃЈ3ЃЉОиаЮ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉНЋМИКЮЬѕМўгУзјБъБэЪОГіРДЃЌЛЏМђМДПЩЃЛЃЈ2ЃЉЩшГіжБЯпЗНГЬЃЌСЊСЂЭждВЃЌЕУЕННЛЕузјБъжЎМфЕФЙиЯЕЃЌИљОнСтаЮПЩЕУЖдНЧЯпДЙжБЃЌРћгУЯђСПДІРэЃЛЃЈ3ЃЉаДГіУцЛ§ЃЌРћгУЛЛдЊЗЈЧѓЦфзюДѓжЕЃЌШЗЖЈmЕФжЕЃЌМДПЩХаЖЈЫФБпаЮЕФаЮзДДѓаЁЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшЕу![]() ЃЌгЩЬтвтЃК
ЃЌгЩЬтвтЃК ![]() МД
МД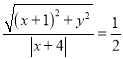 ЃЌЫљвд
ЃЌЫљвд![]() ЛЏМђЕУЃК
ЛЏМђЕУЃК ![]() МДЮЊЧњЯпEЕФЗНГЬ
МДЮЊЧњЯпEЕФЗНГЬ
ЃЈ2ЃЉжБЯпABВЛФмЦНаагкxжсЃЌЙЪЩшжБЯпABЕФЗНГЬЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]()
гЩ![]() ЕУ
ЕУ![]() ЃЌ Ыљвд
ЃЌ Ыљвд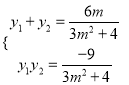 ЂхЂй
ЂхЂй
СЌНсOAЃЌOBЃЌШєABCDЮЊСтаЮЃЌдђ![]() МД
МД![]()
гж![]() ЃЌЫљвдга
ЃЌЫљвдга
![]() ЃЌДњШыЂйЪНЕУ
ЃЌДњШыЂйЪНЕУ![]() ЃЌЮоНтЃЌЙЪABCDВЛФмЪЧСтаЮ.
ЃЌЮоНтЃЌЙЪABCDВЛФмЪЧСтаЮ.
ЃЈ3ЃЉгЩЬтжЊ![]() ЃЌЫљвд
ЃЌЫљвд![]()
Щш![]() ЃЌ
ЃЌ 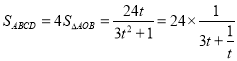
Сю![]() ПЩжЊЕБ
ПЩжЊЕБ![]() ЪБ
ЪБ![]() газюаЁжЕМДУцЛ§газюжЕЃЌДЫЪБ
газюаЁжЕМДУцЛ§газюжЕЃЌДЫЪБ![]() ЃЌМД
ЃЌМД![]() жсЃЌЫљвдABCDЮЊОиаЮ.
жсЃЌЫљвдABCDЮЊОиаЮ.

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИЁОЬтФПЁПЮЊСЫбаОПМвгУНЮГЕдкИпЫйЙЋТЗЩЯЕФГЕЫйЧщПіЃЌНЛЭЈВПУХЖд![]() УћМвгУНЮГЕМнЪЛдБНјааЕїВщЃЌЕУЕНЦфдкИпЫйЙЋТЗЩЯааЪЛЪБЕФЦНОљГЕЫйЧщПіЮЊЃКдк
УћМвгУНЮГЕМнЪЛдБНјааЕїВщЃЌЕУЕНЦфдкИпЫйЙЋТЗЩЯааЪЛЪБЕФЦНОљГЕЫйЧщПіЮЊЃКдк![]() УћФаадМнЪЛдБжаЃЌЦНОљГЕЫйГЌЙ§
УћФаадМнЪЛдБжаЃЌЦНОљГЕЫйГЌЙ§![]()
![]() ЕФга
ЕФга![]() ШЫЃЌВЛГЌЙ§
ШЫЃЌВЛГЌЙ§![]()
![]() ЕФга
ЕФга![]() ШЫЃЛдк
ШЫЃЛдк![]() УћХЎадМнЪЛдБжаЃЌЦНОљГЕЫйГЌЙ§
УћХЎадМнЪЛдБжаЃЌЦНОљГЕЫйГЌЙ§![]()
![]() ЕФга
ЕФга![]() ШЫЃЌВЛГЌЙ§
ШЫЃЌВЛГЌЙ§![]()
![]() ЕФга
ЕФга![]() ШЫ.
ШЫ.
ЃЈЂёЃЉЭъГЩЯТУцЕФСаСЊБэЃЌВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊЦНОљГЕЫйГЌЙ§100
ЕФАбЮеШЯЮЊЦНОљГЕЫйГЌЙ§100![]() гыадБ№гаЙиЃЛ
гыадБ№гаЙиЃЛ
ЦНОљГЕЫйГЌЙ§ | ЦНОљГЕЫйВЛГЌЙ§ | КЯМЦ | |
ФаадМнЪЛШЫЪ§ | |||
ХЎадМнЪЛШЫЪ§ | |||
КЯМЦ |
ЃЈЂђЃЉдкБЛЕїВщЕФМнЪЛдБжаЃЌАДЗжВуГщбљЕФЗНЗЈДгЦНОљГЕЫйВЛГЌЙ§![]()
![]() ЕФШЫжаГщШЁ
ЕФШЫжаГщШЁ![]() ШЫЃЌдйДгет
ШЫЃЌдйДгет![]() ШЫжаВЩгУМђЕЅЫцЛњГщбљЕФЗНЗЈЫцЛњГщШЁ
ШЫжаВЩгУМђЕЅЫцЛњГщбљЕФЗНЗЈЫцЛњГщШЁ![]() ШЫЃЌЧѓет
ШЫЃЌЧѓет![]() ШЫЧЁКУЮЊ
ШЫЧЁКУЮЊ![]() УћФаЩњЁЂ
УћФаЩњЁЂ![]() УћХЎЩњЕФИХТЪ.
УћХЎЩњЕФИХТЪ.
ВЮПМЙЋЪНгыЪ§ОнЃК![]() ЃЌЦфжа
ЃЌЦфжа![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |