题目内容
15.若方程|x2-2x-1|-t=0有四个不同的实数根x1,x2,x3,x4,且x1<x2<x3<x4,则2(x4-x1)+(x3-x2)的取值范围是(4$\sqrt{2}$,8+2$\sqrt{2}$).分析 方程|x2-2x-1|-t=0有四个不同的实数根x1,x2,x3,x4,实际上是抛物线y=|x2-2x-1|和直线y=t的四个不同的交点.根据根与系数的关系和不等式的性质进行解答.
解答 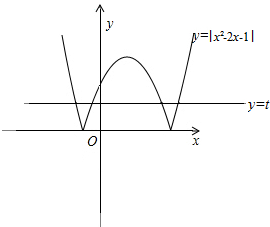 解:如图,由|x2-2x-1|-t=0得到:t=|(x-1)2-2|,则0<t<2.
解:如图,由|x2-2x-1|-t=0得到:t=|(x-1)2-2|,则0<t<2.
∴2<2+t<4.0<2-t<2.
∴4$\sqrt{2}$<4$\sqrt{2+t}$<8,0<2$\sqrt{2-t}$<2$\sqrt{2}$,
∴4$\sqrt{2}$<4$\sqrt{2+t}$+2$\sqrt{2-t}$<8+2$\sqrt{2}$.
∵方程|x2-2x-1|-t=0有四个不同的实数根x1,x2,x3,x4,x1<x2<x3<x4,
∴x1+x4=x2+x3=2,x1•x4=-1-t,x2•x3=-1+t,
∴2(x4-x1)+(x3-x2)
=2$\sqrt{({x}_{1}+{x}_{4})^{2}-4{x}_{1}{x}_{4}}$+$\sqrt{({x}_{2}+{x}_{3})^{2}-4{x}_{2}{x}_{3}}$
=2$\sqrt{4+4(1+t)}$+$\sqrt{4-4(-1+t)}$
=4$\sqrt{2+t}$+2$\sqrt{2-t}$,
∴4$\sqrt{2}$<2(x4-x1)+(x3-x2)<8+2$\sqrt{2}$.
故答案是:(4$\sqrt{2}$,8+2$\sqrt{2}$).
点评 本题主要考查一元二次方程根的情况和含有绝对值的函数的解法,考查基础知识的综合运用能力,以及数形结合的思想,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10.已知全集U={1,2,3,4,5},集合M={3,4,5},N={1,2,5},则集合{1,2}可以表示为( )
| A. | M∩N | B. | (∁UM)∩N | C. | M∩(∁UN) | D. | (∁UM)∩(∁UN) |
20.已知i为虚数单位,复数z=a+bi(a,b∈R)的虚部b记作Im(z),则Im($\frac{1}{1+i}$)=( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
7.在各项都为正数的等差数列{an}中,若a1+a2+…+a10=30,则a5•a6的最大值等于( )
| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
5.已知a,b∈R,则命题“若a2+b2=0,则a=0或b=0”的否命题是( )
| A. | 若a2+b2≠0,则a≠0且b≠0 | B. | 若a2+b2≠0,则a≠0或b≠0 | ||
| C. | 若a≠0且b≠0,则a2+b2≠0 | D. | 若a≠0或b≠0,则a2+b2≠0 |
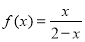 ,
, 的值域是 .
的值域是 .