题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x,-2≤x≤0}\\{ln\frac{1}{x+1},0≤x≤2}\end{array}\right.$,若g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则实数a的取值范围是$\frac{ln3}{3}$≤a<$\frac{1}{e}$.分析 化简|f(x)|=$\left\{\begin{array}{l}{{x}^{2}-2x,-2≤x≤0}\\{ln(x+1),0<x≤2}\end{array}\right.$,从而化g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点为函数|f(x)|与函数y=ax+a的图象有3个不同的交点;作函数的图象,由数形结合求实数a的取值范围.
解答 解:∵f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x,-2≤x≤0}\\{ln\frac{1}{x+1},0≤x≤2}\end{array}\right.$,
∴|f(x)|=$\left\{\begin{array}{l}{{x}^{2}-2x,-2≤x≤0}\\{ln(x+1),0<x≤2}\end{array}\right.$,
∵g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,
∴函数|f(x)|与函数y=ax+a的图象有3个不同的交点;
作函数|f(x)|与函数y=ax+a的图象如下,
图中A(-1,0),B(2,ln3),
故此时直线AB的斜率k=$\frac{ln3-0}{2+1}$=$\frac{ln3}{3}$;
当直线AB与f(x)=ln(x+1)相切时,设切点为(x,ln(x+1));
则$\frac{ln(x+1)-0}{x-(-1)}$=$\frac{1}{x+1}$,
解得,x=e-1;
此时直线AB的斜率k=$\frac{1}{e}$;
结合图象可知,
$\frac{ln3}{3}$≤a<$\frac{1}{e}$;
故答案为:$\frac{ln3}{3}$≤a<$\frac{1}{e}$.
点评 本题考查了函数的零点与函数的图象的关系,同时考查了函数的化简与导数的应用,属于中档题.

| A. | ∅ | B. | {1,4} | C. | M | D. | {2,7} |

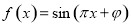 的部分图象如图所示,点
的部分图象如图所示,点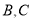 是该图象与
是该图象与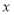 轴的交点,过点
轴的交点,过点 的直线与该图象交于
的直线与该图象交于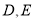 两点,则
两点,则 的值为( )
的值为( )

 D.2
D.2



