题目内容
7.在各项都为正数的等差数列{an}中,若a1+a2+…+a10=30,则a5•a6的最大值等于( )| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
分析 利用a1+a2+…+a10=30,求出a5+a6=6,再利用基本不等式,求出a5•a6的最大值.
解答 解:由题设,a1+a2+a3+…+a10=5(a1+a10)=5(a5+a6)=30
所以a5+a6=6,
又因为等差数列{an}各项都为正数,所以a5a6≤$(\frac{{a}_{5}+{a}_{6}}{2})^{2}$=9,
当且仅当a5=a6=3时等号成立,
所以a5•a6的最大值等于9,
故选C.
点评 本题考查等差数列的性质,考查基本不等式的运用,求出a5+a6=6是关键.

练习册系列答案
相关题目
2.已知命题p:函数f(x)=ln(ex-x+a2-10)(e为自然对数的底数)的值域为R,命题q:${∫}_{0}^{a}$($\sqrt{{a}^{2}-{x}^{2}}$+$\frac{1}{x+1}$)dx>$\frac{π}{4}$+ln2.若命题“p∨q”为真命题,命题“p∧q”为假命题,那么实数a的取值范围是( )
| A. | (1,3] | B. | (-∞,-3) | C. | [-3,1]∪(3,+∞) | D. | (-∞,1]∪(3,+∞) |
12.已知集合M={1,4,7},M∪N=M,则集合N不可能是( )
| A. | ∅ | B. | {1,4} | C. | M | D. | {2,7} |
16.等差数列{an}的前n项和为Sn,若a2+a7+a12=60,则S13的值是( )
| A. | 130 | B. | 20 | C. | 260 | D. | 150 |
17.已知直线y=2(x-1)与抛物线C:y2=4x交于A,B两点,点M(-1,m),若$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\overrightarrow{0}$,则m的值为( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 0 |
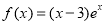 的单调递减区间是( )
的单调递减区间是( ) B.
B.
 D.
D.