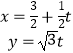题目内容

【题目】执行如图所示的程序框图后，记“输出是好点”为事件A．

（1）若为区间内的整数值随机数，为区间内的整数值随机数，求事件A发生的概率；

（2）若为区间内的均匀随机数，为区间内的均匀随机数，求事件A发生的概率．

【答案】（1）；（2）

【解析】

（1）由题意，若为区间[0，5]内的整数值随机数，为区间[0，2]内的整数值随机数，则可产生6×3＝18个点，事件A发生，则，求出事件数，然后利用古典概型概率计算公式求解；

（2）由题意求出点（，）所构成的矩形面积，再由线性规划知识求出满足的区域面积，由测度比是面积比求概率即可．

（1）由题意，若为区间内的整数值随机数，为区间内的整数值随机数，则可产生个点，

事件A发生，则，好点为，共12个点，

∴；

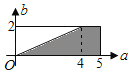
（2）由题意，试验的全部结果构成的区域，其面积为10；

构成事件A的区域，其面积为，

∴．

练习册系列答案
相关题目

【题目】高一某班级在学校数学嘉年华活动中推出了一款数学游戏，受到大家的一致追捧.游戏规则如下：游戏参与者连续抛掷一颗质地均匀的骰子，记第i次得到的点数为，若存在正整数n，使得，则称为游戏参与者的幸运数字。

（I）求游戏参与者的幸运数字为1的概率；

（Ⅱ）求游戏参与者的幸运数字为2的概率，

【题目】已知函数
（1）当a=1时，求函数f（x）在x=e﹣1处的切线方程；
（2）当 时，讨论函数f（x）的单调性；
（3）若x＞0，求函数 的最大值．

【题目】为了研究“晚上喝绿茶与失眠”有无关系，调查了100名人士，得到下面的列联表：

失眠

不失眠

合计

晚上喝绿茶

16

40

56

晚上不喝绿茶

5

39

44

合计

21

79

100

由已知数据可以求得：，则根据下面临界值表：

0.050

0.010

0.001

3.841

6.635

10.828

可以做出的结论是（ ）

A. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠有关”

B. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠无关”

C. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠有关”

D. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠无关”

【题目】若以直角坐标系xOy的O为极点，Ox为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程是ρ= ．
（1）将曲线C的极坐标方程化为直角坐标方程，并指出曲线是什么曲线；
（2）若直线l的参数方程为 （t为参数）当直线l与曲线C相交于A，B两点，求| |

【题目】自2016年1月1日起，我国全面二孩政策正式实施，这次人口与生育政策的历史性调整，使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题．为了解针对产假的不同安排方案形成的生育意愿，某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查，得到如下数据：

产假安排（单位：周）

14

15

16

17

18

有生育意愿家庭数

4

8

16

20

26


（1）若用表中数据所得的频率代替概率，面对产假为14周与16周，估计某家庭有生育意愿的概率分别为多少？
（2）假设从5种不同安排方案中，随机抽取2种不同安排分别作为备选方案，然后由单位根据单位情况自主选择． ①求两种安排方案休假周数和不低于32周的概率；
②如果用ξ表示两种方案休假周数和．求随机变量ξ的分布及期望．

【题目】函数f（x）=sinωx（＞0）的图象向右平移 个单位得到函数y=g（x）的图象，并且函数g（x）在区间[ ， ]上单调递增，在区间[ ]上单调递减，则实数ω的值为（ ）
A.
B.
C.2
D.

【题目】如图所示，有、、三座城市，城在城的正西方向，且两座城市之间的距离为；城在城的正北方向，且两座城市之间的距离为.由城到城只有一条公路，甲有急事要从城赶到城，现甲先从城沿公路步行到点（不包括、两点）处，然后从点处开始沿山路赶往城.若甲在公路上步行速度为每小时，在山路上步行速度为每小时，设（单位：弧度），甲从城赶往城所花的时间为（单位：）.

（1）求函数的表达式，并求函数的定义域；

（2）当点在公路上何处时，甲从城到达城所花的时间最少，并求所花的最少的时间的值.

【题目】设函数f（x）定义域为R，f（﹣x）=f（x），f（x）=f（2﹣x），当x∈[0，1]时，f（x）=x3 ， 则函数g（x）=|cos（πx）|﹣f（x）在区间[﹣ ， ]上的所有零点的和为 ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网