题目内容
【题目】若以直角坐标系xOy的O为极点，Ox为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程是ρ= 
．
（1）将曲线C的极坐标方程化为直角坐标方程，并指出曲线是什么曲线；
（2）若直线l的参数方程为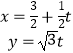 
（t为参数）当直线l与曲线C相交于A，B两点，求| 
|
【答案】
（1）解：∵ρ= 
，∴ρ2sin2θ=6ρcosθ，
∴曲线C的直角坐标方程为y2=6x．曲线为以（ 
，0）为焦点，开口向右的抛物线．
（2）解：直线l的参数方程可化为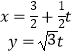 
，代入y2=6x得t2﹣4t﹣12=0．
解得t1=﹣2，t2=6．
∴| 
|=|t1﹣t2|=8
【解析】（1）将极坐标方程两边同乘ρ，去分母即可得到直角坐标方程；（2）写出直线l参数方程的标准形式，代入曲线C的普通方程，根据参数的几何意义得出|AB|．
练习册系列答案
相关题目
