Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņő™Ńň—–ĺŅ°įÕŪ…Ōļ»¬Ő≤Ť”Ž ß√Ŗ°Ī”–őřĻōŌĶ£¨Ķų≤ťŃň100√Ż»ň Ņ£¨Ķ√ĶĹŌ¬√śĶńŃ–Ń™ĪŪ£ļ
ß√Ŗ | ≤Ľ ß√Ŗ | ļŌľ∆ | |
ÕŪ…Ōļ»¬Ő≤Ť | 16 | 40 | 56 |
ÕŪ…Ō≤Ľļ»¬Ő≤Ť | 5 | 39 | 44 |
ļŌľ∆ | 21 | 79 | 100 |
”…“—÷™ żĺ›Ņ…“‘«ůĶ√£ļ![]() £¨‘Úłýĺ›Ō¬√śŃŔĹÁ÷ĶĪŪ£ļ
£¨‘Úłýĺ›Ō¬√śŃŔĹÁ÷ĶĪŪ£ļ
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
Ņ…“‘◊Ų≥ŲĶńĹŠ¬Ř «£® £©
A. ‘ŕ∑łīŪőůĶńłŇ¬ ≤Ľ≥¨Ļż0.01Ķń«įŐŠŌ¬»Ōő™°įÕŪ…Ōļ»¬Ő≤Ť”Ž ß√Ŗ”–Ļō°Ī
B. ‘ŕ∑łīŪőůĶńłŇ¬ ≤Ľ≥¨Ļż0.01Ķń«įŐŠŌ¬»Ōő™°įÕŪ…Ōļ»¬Ő≤Ť”Ž ß√ŖőřĻō°Ī
C. ‘ŕ∑łīŪőůĶńłŇ¬ ≤Ľ≥¨Ļż0.05Ķń«įŐŠŌ¬»Ōő™°įÕŪ…Ōļ»¬Ő≤Ť”Ž ß√Ŗ”–Ļō°Ī
D. ‘ŕ∑łīŪőůĶńłŇ¬ ≤Ľ≥¨Ļż0.05Ķń«įŐŠŌ¬»Ōő™°įÕŪ…Ōļ»¬Ő≤Ť”Ž ß√ŖőřĻō°Ī
°ĺīūįł°ŅC
°ĺĹ‚őŲ°Ņ∑÷őŲ£ļłýĺ›Ő‚“‚łÝ∂®Ķń![]() Ķń÷Ķ£¨”ŽŃŔĹÁ÷ĶĪŪĶń żĺ›Ī»ĹŌ£¨ľīŅ…Ķ√ĶĹīūįł.
Ķń÷Ķ£¨”ŽŃŔĹÁ÷ĶĪŪĶń żĺ›Ī»ĹŌ£¨ľīŅ…Ķ√ĶĹīūįł.
ŌÍĹ‚£ļ”…Ő‚“‚£¨÷™![]() £¨
£¨
łýĺ›ŃŔĹÁ÷ĶĪŪ£ļŅ…Ķ√![]() £¨
£¨
ňý“‘Ņ…Ķ√‘ŕ∑łīŪőůĶńłŇ¬ ≤Ľ≥¨Ļż![]() Ķń«įŐŠŌ¬»Ōő™°įÕŪ…Ōļ»¬Ő≤Ť”Ž ß√Ŗ”–Ļō°Ī£¨Ļ —°C.
Ķń«įŐŠŌ¬»Ōő™°įÕŪ…Ōļ»¬Ő≤Ť”Ž ß√Ŗ”–Ļō°Ī£¨Ļ —°C.

°ĺŐ‚ńŅ°Ņń≥…Ő≥°ĺŔ––”–ĹĪīŔŌķĽÓ∂Į£¨ĻňŅÕĻļ¬Ú“Ľ∂®Ĺū∂ÓĶń…Ő∆∑ļůľīŅ…≤őľ”“Ľīő≥ťĹĪ.ňś◊Ň≥ťĹĪĽÓ∂ĮĶń”––ßŅ™’Ļ£¨≤ő”Ž≥ťĹĪĽÓ∂ĮĶń»ň ż‘Ĺņī‘Ĺ∂ŗ£¨ł√…Ő≥°∂‘«į5Őž≥ťĹĪĽÓ∂ĮĶń»ň żĹÝ––Õ≥ľ∆£¨yĪŪ ĺĶŕxŐž≤őľ”≥ťĹĪĽÓ∂ĮĶń»ň ż£¨Ķ√ĶĹÕ≥ľ∆ĪŪ»ÁŌ¬£ļ
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
ĺ≠ĻżĹÝ“Ľ≤ĹÕ≥ľ∆∑÷őŲ£¨∑ĘŌ÷y”ŽxĺŖ”–ŌŖ–‘ŌŗĻōĻōŌĶ.
£®1£©»Űī”’‚5ŐžňśĽķ≥ť»°ŃĹŐž£¨«ů÷Ń…Ŕ”–1Őž≤őľ”≥ťĹĪ»ň ż≥¨Ļż70ĶńłŇ¬ £Ľ
£®2£©«Žłýĺ›…ŌĪŪŐŠĻ©Ķń żĺ›£¨”√◊Ó–°∂Ģ≥ň∑®«ů≥ŲyĻō”ŕxĶńŌŖ–‘ĽōĻť∑Ĺ≥Ő![]() £¨≤ĘĻņľ∆ł√ĽÓ∂Į≥÷–Ý7Őž£¨Ļ≤”–∂ŗ…Ŕ√ŻĻňŅÕ≤őľ”≥ťĹĪ£Ņ
£¨≤ĘĻņľ∆ł√ĽÓ∂Į≥÷–Ý7Őž£¨Ļ≤”–∂ŗ…Ŕ√ŻĻňŅÕ≤őľ”≥ťĹĪ£Ņ
≤őŅľĻę Ĺľį żĺ›£ļ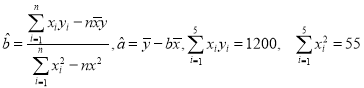 .
.


