题目内容
【题目】如图所示，有
、
、
三座城市，城在城的正西方向，且两座城市之间的距离为
；城在城的正北方向，且两座城市之间的距离为.由城到城只有一条公路
，甲有急事要从城赶到城，现甲先从城沿公路步行到点
（不包括、两点）处，然后从点处开始沿山路
赶往城.若甲在公路上步行速度为每小时
，在山路上步行速度为每小时
，设
（单位：弧度），甲从城赶往城所花的时间为
（单位：
）.
（1）求函数
的表达式，并求函数的定义域；
（2）当点在公路上何处时，甲从城到达城所花的时间最少，并求所花的最少的时间的值.
【答案】（1）
定义域为
（2）点
所在的位置为
处，甲所花最短时间为
.
【解析】试题分析：（1）先在直角三角形中用
表示
，
，再根据时间等于路程除以速度得
，最后根据实际意义得定义域，（2）先求函数导数，再求导函数零点
，列表分析导函数符号变化规律，确定单调性，进而确定最值取法.
试题解析：解：（1）在
中，
，
，
故
.
由图知
，
，故函数
的定义域为
（2）令
则
.
令
，可得
，由
可解得
.
故函数
的增区间为
，减区间为
故当时，函数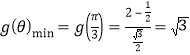
.
故点所在的位置为处，甲所花最短时间为.
练习册系列答案
相关题目
