题目内容
(14分)已知定义在 上的函数
上的函数 ,其中
,其中 为常数.
为常数.
(1)若 ,求证:函数
,求证:函数 在区间
在区间 上是增函数;
上是增函数;
(2)若函数 ,在
,在 处取得最大值,求正数
处取得最大值,求正数 的取值范围.
的取值范围.
 上的函数
上的函数 ,其中
,其中 为常数.
为常数.(1)若
 ,求证:函数
,求证:函数 在区间
在区间 上是增函数;
上是增函数;(2)若函数
 ,在
,在 处取得最大值,求正数
处取得最大值,求正数 的取值范围.
的取值范围.(1)略(2)

解:(1)当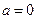 时,
时,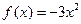 在区间
在区间 上是增函数,
上是增函数,
当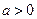 时,
时,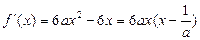 ,
,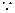
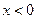 ,
,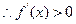
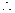 函数
函数 在区间
在区间 上是增函数,
上是增函数,
综上得,函数 在区间
在区间 上是增函数. ………………6分
上是增函数. ………………6分
(2)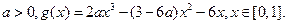
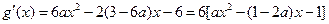
令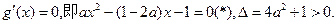 ………………10分
………………10分
设方程(*)的两个根为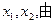 (*)式得
(*)式得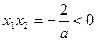 ,不妨设
,不妨设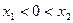 .
.
当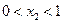 时,
时,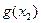 为极小值,所以
为极小值,所以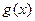 在[0,1]上的最大值只能为
在[0,1]上的最大值只能为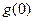 或
或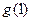 ; ………10分
; ………10分
当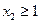 时,由于
时,由于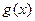 在[0,1]上是单调递减函数,所以最大值为
在[0,1]上是单调递减函数,所以最大值为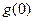 ,
,
所以在[0,1]上的最大值只能为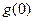 或
或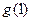 , ……12分
, ……12分
又已知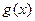 在
在 处取得最大值,所以
处取得最大值,所以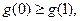
即 . …………14分
. …………14分
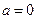 时,
时,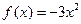 在区间
在区间 上是增函数,
上是增函数,当
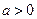 时,
时,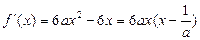 ,
,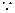
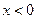 ,
,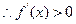
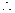 函数
函数 在区间
在区间 上是增函数,
上是增函数,综上得,函数
 在区间
在区间 上是增函数. ………………6分
上是增函数. ………………6分(2)
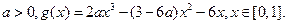
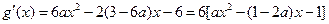
令
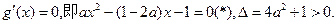 ………………10分
………………10分设方程(*)的两个根为
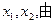 (*)式得
(*)式得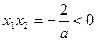 ,不妨设
,不妨设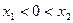 .
.当
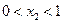 时,
时,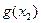 为极小值,所以
为极小值,所以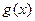 在[0,1]上的最大值只能为
在[0,1]上的最大值只能为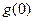 或
或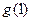 ; ………10分
; ………10分当
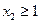 时,由于
时,由于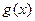 在[0,1]上是单调递减函数,所以最大值为
在[0,1]上是单调递减函数,所以最大值为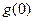 ,
,所以在[0,1]上的最大值只能为
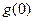 或
或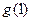 , ……12分
, ……12分又已知
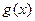 在
在 处取得最大值,所以
处取得最大值,所以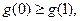
即
 . …………14分
. …………14分
练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为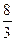 .
.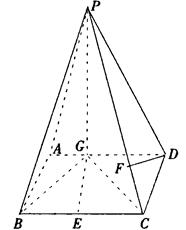 (Ⅱ)求点D到平面PBG的距离;
(Ⅱ)求点D到平面PBG的距离;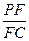 的值.
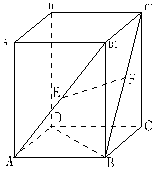
的值.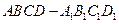 中,E、F
中,E、F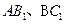 的中点,则以下结论中不成立的是
的中点,则以下结论中不成立的是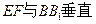
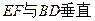
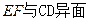
 的所有棱长均为
的所有棱长均为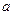 ,侧面
,侧面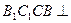 底面
底面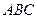 ,且
,且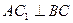 .
.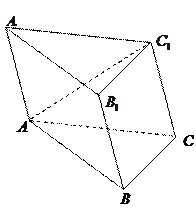
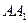 与
与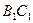 间的距离;
间的距离;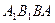 与底面
与底面 是以
是以 为半径的球
为半径的球 的小圆,若圆
的小圆,若圆 和球
和球 的比为
的比为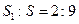 ,则圆心
,则圆心 _____。
_____。
 ,点P是棱DD1的中点,
,点P是棱DD1的中点, ,AB=1,若点Q在侧面
,AB=1,若点Q在侧面 (包括其边界)上运动,且总保持
(包括其边界)上运动,且总保持 ,则动点Q的轨迹是 ( )
,则动点Q的轨迹是 ( )
