Question

【题目】已知函数在点处的切线方程是.

(1)求的值及函数的最大值；

(2)若实数满足.

(i)证明：；

(ii)若，证明：.

Answer 1

【答案】(1)；0.

(2) （ⅰ）证明见解析；（ⅱ）证明见解析.

【解析】分析：第一问利用题中所给的条件，结合导数的几何意义以及切点应该在切线上，建立关于的等量关系式，解方程组求得的值，从而确定出函数的解析式，利用导数研究函数的单调性，从而求导函数的最大值，第二问将问题转化，利用导数，构造函数，证得结果.

详解：（Ⅰ），

由题意有，解得．

故，，

，所以在为增函数，在为减函数．

故有当时，．

（Ⅱ）证明：

（ⅰ），

由（Ⅰ）知，所以，即.

又因为（过程略），所以，故.

（ⅱ）法一：

由（1）知

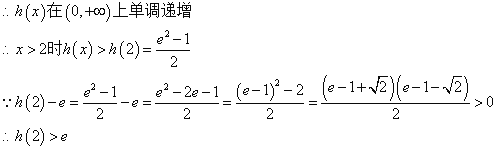
法二：，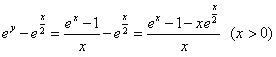

构造函数，，

因为，所以，

即当时，，所以在为增函数，

所以，即，故