Question

【题目】已知四棱锥P﹣ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面 ABCD，且PA=AD=DB= ，AB=1，M是PB的中点．
（1）证明：面PAD⊥面PCD；
（2）求AC与PB所成的角；
（3）求平面AMC与平面BMC所成二面角的大小．

Answer 1

【答案】
（1）证明：∵PA⊥面ABCD，CD⊥AD，

∴由三垂线定理得：CD⊥PD．

因而，CD与面PAD内两条相交直线AD，PD都垂直，

∴CD⊥面PAD．

又CD面PCD，∴面PAD⊥面PCD

（2）解：过点B作BE∥CA，且BE=CA，则∠PBE是AC与PB所成的角．

连接AE，可知AC=CB=BE=AE= ，

又AB=2，所以四边形ACBE为正方形．

由PA⊥面ABCD，得∠PEB=90°

在Rt△PEB中，BE=a2=3b2，PB= ，

∴cos∠PBE= = ．

∴AC与PB所成的角为arccos

（3）证明：作AN⊥CM，垂足为N，连接BN．

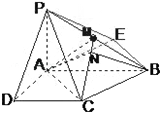
在Rt△PAB中，AM=MB，又AC=CB，

∴△AMC≌△BMC，

∴BN⊥CM，故∠ANB为所求二面角的平面角

∵CB⊥AC，

由三垂线定理，得CB⊥PC，

在Rt△PCB中，CM=MB，所以CM=AM．

在等腰三角形AMC中，ANMC= AC，

∴AN= 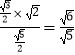．∴AB=2，

∴cos∠ANB= =﹣ ，

故平面AMC与平面BMC所成二面角的大小为arccos（﹣ ）．

【解析】（1）由三垂线定理得CD⊥PD，从而CD⊥面PAD，再由CD面PCD，能证明面PAD⊥面PCD． （2）过点B作BE∥CA，且BE=CA，则∠PBE是AC与PB所成的角． 连接AE，推导出四边形ACBE为正方形，由此能求出AC与PB所成的角．（3）作AN⊥CM，垂足为N，连接BN，则∠ANB为所求二面角的平面角，由此能求出平面AMC与平面BMC所成二面角的大小．
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识，掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系，以及对平面与平面垂直的判定的理解，了解一个平面过另一个平面的垂线，则这两个平面垂直．