题目内容
【题目】如图是一块地皮![]() ,其中
,其中![]() ,
, ![]() 是直线段,曲线段
是直线段,曲线段![]() 是抛物线的一部分,且点
是抛物线的一部分,且点![]() 是该抛物线的顶点,
是该抛物线的顶点, ![]() 所在的直线是该抛物线的对称轴.经测量,
所在的直线是该抛物线的对称轴.经测量, ![]() km,
km, ![]() km,
km, ![]() .现要从这块地皮中划一个矩形
.现要从这块地皮中划一个矩形![]() 来建造草坪,其中点
来建造草坪,其中点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() ,
, ![]() 在直线段
在直线段![]() 上,点
上,点![]() 在直线段
在直线段![]() 上,设
上,设![]() km,矩形草坪
km,矩形草坪![]() 的面积为
的面积为![]() km2.
km2.
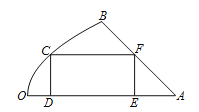
(1)求![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 为多少时,矩形草坪
为多少时,矩形草坪![]() 的面积最大?
的面积最大?
【答案】(1)![]() ,定义域为
,定义域为![]() ;
;
(2)当![]() 时,矩形草坪
时,矩形草坪![]() 的面积最大.
的面积最大.
【解析】试题分析:
(1)由题意可得函数的解析式为![]() ,定义域为
,定义域为![]() ;
;
(2)对函数求导,结合导函数与原函数的关系可得当![]() 时,矩形草坪
时,矩形草坪![]() 的面积最大.
的面积最大.
试题解析:
(1)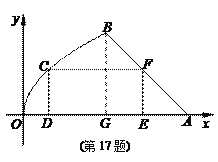
以O为原点,OA边所在直线为![]() 轴,建立
轴,建立
如图所示的平面直角坐标系,
过点![]() 作
作![]() 于点
于点![]() ,
,
在直角![]() 中,
中, ![]() ,
, ![]() ,
,
所以![]() ,又因为
,又因为![]() ,
,
所以![]() ,则
,则![]() ,
,
设抛物线OCB的标准方程为![]() ,
,
代入点![]() 的坐标,得
的坐标,得![]() ,
,
所以抛物线的方程为![]() .
.
因为![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以![]()
![]() ,定义域为
,定义域为![]() .
.
(2)![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 在
在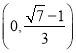 上单调增;
上单调增;
当![]() 时,
时, ![]() ,
, ![]() 在
在 上单调减.
上单调减.
所以当![]() 时,
时, ![]() 取得极大值,也是最大值.
取得极大值,也是最大值.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
