题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点.
上的动点.
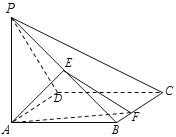
(1)平面![]() 与平面
与平面![]() 是否互相垂直?如果垂直,请证明;如果不垂直,请说明理由.
是否互相垂直?如果垂直,请证明;如果不垂直,请说明理由.
(2)若![]() ,
,![]() 为线段
为线段![]() 的三等分点,求多面体
的三等分点,求多面体![]() 的体积.
的体积.
【答案】(1)互相垂直,证明见解析(2)![]() 或
或![]() .
.
【解析】
(1)证明![]() 平面
平面![]() 中的
中的![]() 即可.
即可.
(2)利用多面体![]() 的体积为
的体积为![]() ,分
,分![]() 为线段
为线段![]() 的两个不同的三等分点进行求解即可.
的两个不同的三等分点进行求解即可.
解法一:(1)平面![]() 与平面
与平面![]() 互相垂直,
互相垂直,
理由如下:
因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() 为正方形,所以
为正方形,所以![]()
又![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
因为![]() ,
,![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
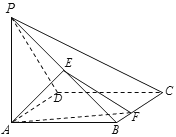
(2)因为![]() 底面
底面![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,
所以点![]() 到底面
到底面![]() 的距离为
的距离为![]()
![]() ,
,
则![]() ,
,
又![]() 为线段
为线段![]() 的三等分点,
的三等分点,
当![]() 时,
时,![]() ,
,
所以多面体![]() 的体积为
的体积为![]() ;
;
当![]() 时,
时,![]() ,
,
所以多面体![]() 的体积为
的体积为![]() .
.
综上,多面体![]() 的体积为
的体积为![]() 或
或![]() .
.
解法二:(1)平面![]() 与平面
与平面![]() 互相垂直,
互相垂直,
理由如下:
因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 底面
底面![]() ,
,
又平面![]() 底面
底面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
因为![]() ,
,![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]()
(2)同解法一.

 阅读快车系列答案
阅读快车系列答案【题目】某租车公司给出的财务报表如下:
年度 项目 | 2014年 (1-12月) | 2015年 (1-12月) | 2016年 (1-11月) |
接单量(单) | 14463272 | 40125125 | 60331996 |
油费(元) | 214301962 | 581305364 | 653214963 |
平均每单油费 | 14.82 | 14.49 | |
平均每单里程 | 15 | 15 | |
每公里油耗 | 0.7 | 0.7 | 0.7 |
有投资者在研究上述报表时,发现租车公司有空驶情况,并给出空驶率的计算公式为![]() .
.
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里).
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了![]() 人,他们年龄的频数分布及支持“生育二胎”人数如下表:
人,他们年龄的频数分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
支持“生二胎” |
|
|
|
|
|
|
(1)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为以
的把握认为以![]() 岁为分界点对“生育二胎放开”政策的支持度有差异;
岁为分界点对“生育二胎放开”政策的支持度有差异;
年龄不低于 | 年龄低于 | 合计 | |
支持 |
|
| |
不支持 |
|
| |
合计 |
(2)若对年龄在![]() 的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据:![]() ,
,![]() ,
,![]() .
.