题目内容
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了![]() 人,他们年龄的频数分布及支持“生育二胎”人数如下表:
人,他们年龄的频数分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
支持“生二胎” |
|
|
|
|
|
|
(1)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为以
的把握认为以![]() 岁为分界点对“生育二胎放开”政策的支持度有差异;
岁为分界点对“生育二胎放开”政策的支持度有差异;
年龄不低于 | 年龄低于 | 合计 | |
支持 |
|
| |
不支持 |
|
| |
合计 |
(2)若对年龄在![]() 的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据:![]() ,
,![]() ,
,![]() .
.
【答案】(1)没有,理由见解析;(2)![]() .
.
【解析】
(1)根据题中数据完善![]() 列联表,计算出
列联表,计算出![]() 的观测值,利用参考数据即可对题中的结论进行判断;
的观测值,利用参考数据即可对题中的结论进行判断;
(2)将所选![]() 人中支持“生育二胎放开”的
人中支持“生育二胎放开”的![]() 人记为
人记为![]() 、
、![]() 、
、![]() 、
、![]() ,不支持“生育二胎放开”的
,不支持“生育二胎放开”的![]() 人记为
人记为![]() ,利用列举法列举出所有的基本事件,并确定事件“所抽取的两人都支持“生育二胎放开””所包含的基本事件,利用古典概型的概率公式可计算出结果.
,利用列举法列举出所有的基本事件,并确定事件“所抽取的两人都支持“生育二胎放开””所包含的基本事件,利用古典概型的概率公式可计算出结果.
(1)根据题中数据,![]() 列联表如下:
列联表如下:
年龄不低于 | 年龄低于 | 合计 | |
支持 |
|
|
|
不支持 |
|
|
|
合计 |
|
|
|
![]() ,
,
因此,没有![]() 的把握认为以
的把握认为以![]() 岁为分界点对“生育二胎放开”政策的支持度有差异;
岁为分界点对“生育二胎放开”政策的支持度有差异;
(2)由题意可知,年龄在![]() 的有
的有![]() 人,其中支持“生育二胎放开”的有
人,其中支持“生育二胎放开”的有![]() 人,分别记为
人,分别记为![]() 、
、![]() 、
、![]() 、
、![]() ,不支持“生育二胎放开”的
,不支持“生育二胎放开”的![]() 人记为
人记为![]() ,
,
所有的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种.
种.
事件“所抽取的两人都支持“生育二胎放开””包含的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种,
种,
由古典概型的概率公式可知,所抽取的两人都支持“生育二胎放开”的概率为![]() .
.

 名校课堂系列答案
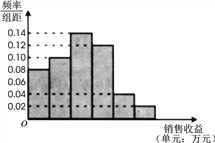
名校课堂系列答案【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.