Question

【题目】设命题p：函数f(x)＝lg(ax2－x＋ a)的定义域为R；命题q：不等式3x－9x＜a对一切正实数均成立．如果命题“p∨q”为真命题，“p∧q”为假命题，求实数a的取值范围( )．
A.0≤a＜1
B.0≤a
C.a≤1
D.0≤a≤1

Answer 1

【答案】D
【解析】若命题p为真，即ax2－x＋ a＞0恒成立，
则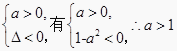
令y＝3x－9x＝－＋ ，
由x＞0得3x＞1，
∴y＝3x－9x的值域为(－∞，0)．
∴若命题q为真，则a≥0.
由命题“p∨q”为真，“p∧q”为假，得命题p、q一真一假，当p真q假时，a不存在；当p假q真时，0≤a≤1.
∴a的取值范围是0≤a≤1.故选D.
【考点精析】利用四种命题的真假关系对题目进行判断即可得到答案，需要熟知一个命题的真假与其他三个命题的真假有如下三条关系：(原命题 逆否命题)①、原命题为真，它的逆命题不一定为真;②、原命题为真，它的否命题不一定为真;③、原命题为真，它的逆否命题一定为真．