题目内容
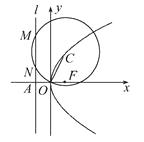
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.
交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.
(1)求点Q的坐标;
(2)当P为抛物线上位于线段AB下方(含A、B)的动点时,求ΔOPQ面积的最大值.
【答案】
(1)
【解答】解方程组  得
得 ![]() 或
或![]()
即A(-4,-2),B(8,4),从而AB的中点为M(2,1).由kAB= ![]() ,直线AB的垂直平分线方程
,直线AB的垂直平分线方程
y-1= ![]() (x-2).令y=-5,得x=5,∴Q(5,-5).
(x-2).令y=-5,得x=5,∴Q(5,-5).
(2)
【解答】直线OQ的方程为x+y=0,设P(x, ![]() x2-4).∵点P到直线OQ的距离
x2-4).∵点P到直线OQ的距离![]() ,
,
![]() ,
,
∴![]() .
.
∵P为抛物线上位于线段AB下方的点,且P不在直线OQ上,∴-4≤x<4 ![]() -4或4
-4或4 ![]() -4<x≤8.
-4<x≤8.
∵函数y=x2+8x-32在区间[-4,8]上单调递增,∴当x=8时,ΔOPQ的面积取到最大值30.
【解析】(1)把直线方程抛物线方程联立求得交点A,B的坐标,则AB中点M的坐标可得,利用AB的斜率推断出AB垂直平分线的斜率,进而求得AB垂直平分线的方程,把y=-5代入求得Q的坐标.(2)设出P的坐标,利用P到直线0Q的距离求得三角形的高,利用两点间的距离公式求得QO的长,最后利用三角形面积公式表示出三角形OPQ,利用x的范围和二次函数的单调性求得三角形面积的最大值.

练习册系列答案
相关题目