Question

【题目】【选修4－4：坐标系与参数方程】

已知直线l：ρsin（θ＋）＝m，曲线C：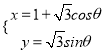

（1）当m＝3时，判断直线l与曲线C的位置关系；

（2）若曲线C上存在到直线l的距离等于的点，求实数m的范围．

Answer 1

【答案】(1)相切（2）[-2,4]

【解析】试题分析：（1）分别化为直角坐标方程，求出圆心到直线的距离d与半径比较即可得出结论．

（2）曲线C上存在到直线l的距离等于的点，可得圆心C（1，0）到直线l的距离d≤r+，解出即可得出．

试题解析：

（1）直线l：ρsin（θ＋）＝m ，化为直角坐标方程：y+x=m，

m=3时，化为：y+x﹣3=0，

曲线C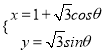： ，利用平方关系化为：（x﹣1）2+y2=3．

圆心C（1，0）到直线l的距离d===r，

因此直线l与曲线C相切．

（2）∵曲线C上存在到直线l的距离等于的点，

∴圆心C（1，0）到直线l的距离d=≤+，解得﹣2≤m≤4．

∴实数m的范围是[﹣2，4]．