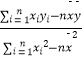题目内容
【题目】判断下列命题是全称命题还是特称命题，并判断其真假；写出这些命题的否定并判断真假.
（1）三角形的内角和为180°；
（2）每个二次函数的图象都开口向下；
（3）存在一个四边形不是平行四边形；
（4）
;
（5）.
【答案】
（1）
【解答】
解：是全称命题且为真命题.
命题的否定：三角形的内角和不全为180°，
即存在一个三角形，它的内角和不等于180°，为假命题.
（2）
【解答】
解：是全称命题且为假命题.
命题的否定：存在一个二次函数的图象开口不向下，为真命题.
（3）
【解答】
解：是特称命题且为真命题.
命题的否定：所有的四边形都是平行四边形，为假命题.
（4）
【解答】
解：是全称命题且为真命题.
由于 
都有 
，故 
， p 为真命题；
： 
， 为假命题
（5）
【解答】
解：是特称命题且为假命题.
因为不存在一个实数 x ，使 
成立， p 为假命题；
： 
， 为真命题.
【解析】命题的否定要与否命题区别开来，全称命题的否定是特称命题，而特称命题的否定是全称命题.
【考点精析】解答此题的关键在于理解全称命题的相关知识，掌握全称命题
：
，
，它的否定
：
，
;全称命题的否定是特称命题．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
