题目内容
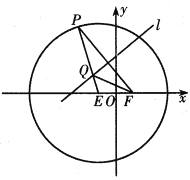
【题目】已知F1，F2是椭圆与双曲线的公共焦点，P是它们的一个公共点，且|PF1|＜|PF2|，线段PF1的垂直平分线经过点F2，若椭圆的离心率为e1，双曲线的离心率为e2，则
的最小值为（ ）
A.2B.﹣2C.6D.﹣6
【答案】B
【解析】
设
，不妨设点
在第二象限，椭圆和曲线的焦点在
轴上，且它们的长半轴为
，实半轴为
，半焦距为
，运用椭圆和双曲线的定义，以及垂直平分线的性质，结合离心率和基本不等式，即可求解.
设，不妨设点在第二象限，
椭圆和曲线的焦点在轴上，且它们的长半轴为，实半轴为，半焦距为，
由椭圆和双曲线的定义可得
，
由线段
的垂直平分线过点
，可得
又由点在第二象限，所以
，即
，所以
，
且， 即
，
又由椭圆和双曲线的离心率，可得
，
则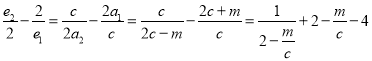
，
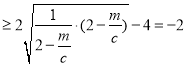当且仅当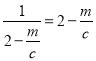
，即
时，上式取得最小值
.
故选：B.
练习册系列答案
相关题目
