Question

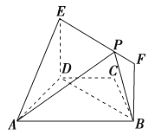
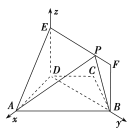
【题目】如图，在梯形ABCD中，AB∥CD，AD＝DC＝CB＝1，∠BCD＝120°，四边形BFED为矩形，平面BFED⊥平面ABCD，BF＝1.

(1)求证：AD⊥平面BFED；

(2)点P在线段EF上运动，设平面PAB与平面ADE所成锐二面角为θ，试求θ的最小值．

Answer 1

【答案】（1）证明见解析 （2）θ最小值为60°

【解析】

（1）在梯形ABCD中，利用勾股定理，得到AD⊥BD，再结合面面垂直的判定，证得DE⊥平面ABCD，即可证得AD⊥平面BFED；

（2）以D为原点，直线DA，DB，DE分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，求得平面PAB与平面ADE法向量，利用向量的夹角公式，即可求解．

（1）证明：在梯形ABCD中，

∵AB∥CD，AD＝DC＝CB＝1，∠BCD＝120°，∴AB＝2.

∴BD2＝AB2＋AD2－2AB·AD·cos 60°＝3.

∴AB2＝AD2＋BD2，∴AD⊥BD.

∵平面BFED⊥平面ABCD，平面BFED∩平面ABCD＝BD，

DE平面BFED，DE⊥DB，∴DE⊥平面ABCD，

∴DE⊥AD，又DE∩BD＝D，∴AD⊥平面BFED.

（1）由(1)知，直线AD，BD，ED两两垂直，故以D为原点，直线DA，DB，DE分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，

令EP＝λ(0≤λ≤)，则D(0,0,0)，A(1,0,0)，B(0，，0)，P(0，λ，1)，

所以＝(－1，，0)，＝(0，λ－，1)．

设n1＝(x，y，z)为平面PAB的法向量，

由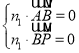得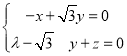，取y＝1，则n1＝(，1，－λ)．

因为n2＝(0,1,0)是平面ADE的一个法向量，

所以cos θ＝＝＝.

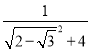因为0≤λ≤，所以当λ＝时，cos θ有最大值，所以θ的最小值为60°.