题目内容
7.已知sinθ•cosθ=$\frac{1}{8}$,且$\frac{π}{4}$<θ<$\frac{π}{2}$,则sinθ=$\frac{\sqrt{5}+\sqrt{3}}{4}$.分析 由已知等式,利用完全平方公式及同角三角函数间基本关系求出sinθ+cosθ与sinθ-cosθ的值,联立即可求出sinθ的值.
解答 解:∵sinθ•cosθ=$\frac{1}{8}$,
∴1+2sinθcosθ=$\frac{5}{4}$,即(sinθ+cosθ)2=$\frac{5}{4}$;1-2sinθcosθ=$\frac{3}{4}$,即(sinθ-cosθ)2=$\frac{3}{4}$,
∵$\frac{π}{4}$<θ<$\frac{π}{2}$,
∴sinθ>cosθ,sinθ-cosθ>0,
∴sinθ+cosθ=$\frac{\sqrt{5}}{2}$,sinθ-cosθ=$\frac{\sqrt{3}}{2}$,
解得:sinθ=$\frac{\sqrt{5}+\sqrt{3}}{4}$,
故答案为:$\frac{\sqrt{5}+\sqrt{3}}{4}$
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
19.设a1,a2,a3,a4∈R+,P=a${\;}_{1}^{2}$+a${\;}_{2}^{2}$+a${\;}_{3}^{2}$+a${\;}_{4}^{2}$,Q=a1a2+a2a3+a3a4+a4a1,则有( )
| A. | P<Q | B. | P>Q | C. | P≤Q | D. | P≥Q |
16.设集合∪=R,M={x||x|<2},N={y|y=2x-1},则(CUM)∪(CUN)=( )
| A. | (-1,2) | B. | (-∞,2] | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-1]∪[2,+∞) |
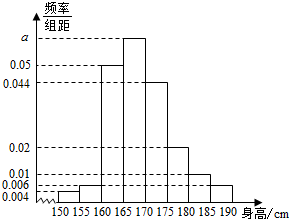 某校从高一年级男生中随机抽取100个样本,将他们的身高(最高189cm,最低150cm)分成八段:[150,155),[155,160),[160,165),…,[185,190)后得到如图的频率分布直方图.
某校从高一年级男生中随机抽取100个样本,将他们的身高(最高189cm,最低150cm)分成八段:[150,155),[155,160),[160,165),…,[185,190)后得到如图的频率分布直方图.