题目内容
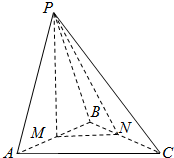
7.如图,已知四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,PA=AB=2,AD=4,M为侧棱PC的中点.
(1)求异面直线AM与PD所成角的余弦值;
(2)求二面角B-PC-D的余弦值.
分析 (1)以A为原点,建立空间直角坐标系A-xyz,求出$\overrightarrow{AM}=(1,2,1),\overrightarrow{PD}=(0,4,-2)$,利用向量的数量积直接求解异面直线AM与PD所成角的余弦值.
(2)求出平面BPC的法向量,平面MBD的一个法向量,利用空间向量的数量积求解二面角B-PC-D的余弦值.
解答 (理科)解:
(1)如图所示,以A为原点,建立空间直角坐标系A-xyz,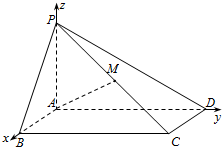
则A(0,0,0),B(2,0,0),D(0,4,0),P(0,0,2),C(2,4,0),M(1,2,1),…2'∵$\overrightarrow{AM}=(1,2,1),\overrightarrow{PD}=(0,4,-2)$,∴$cos<\overrightarrow{AM},\overrightarrow{PD}>=\frac{{\overrightarrow{AM}•\overrightarrow{PD}}}{{|{\overrightarrow{AM}}||{\overrightarrow{PD}}|}}=\frac{0+8-2}{{\sqrt{6}×2\sqrt{5}}}=\frac{{\sqrt{30}}}{10}$,
∴异面直线AM与PD所成角的余弦值为$\frac{{\sqrt{30}}}{10}$…7'
(2)设平面BPC的法向量为$\overrightarrow{m}$=(x,y,z),∵$\overrightarrow{BC}=(0,4,0),\overrightarrow{BP}=(-2,0,2)$,并且$\overrightarrow{m}⊥\overrightarrow{BC},\overrightarrow{m}⊥\overrightarrow{BP}$,∴$\left\{\begin{array}{l}4y=0\\-2x+2z=0\end{array}\right.$,令x=1得z=1,y=0,∴平面MBD的一个法向量为$\overrightarrow{m}$=(1,0,1)…9'
设平面DPC的法向量为$\overrightarrow{n}$=(a,b,c),∵$\overrightarrow{DC}=(2,0,0),\overrightarrow{DP}=(0,-4,2)$,并且$\overrightarrow{n}⊥\overrightarrow{DC},\overrightarrow{n}⊥\overrightarrow{DP}$,∴$\left\{\begin{array}{l}2a=0\\-4b+2c=0\end{array}\right.$,令b=1得c=2,a=0,∴平面MBD的一个法向量为$\overrightarrow{n}$=(0,1,2)…11'
∴$cos<\overrightarrow{m},\overrightarrow{n}>=\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}=\frac{2}{\sqrt{2}•\sqrt{5}}=\frac{\sqrt{10}}{5}$,…13'
∴二面角B-PC-D的余弦值为$-\frac{{\sqrt{10}}}{5}$…14'
点评 本题考查空间向量的数量积的应用,二面角以及异面直线所成角的求法,考查转化思想以及计算能力.

| A. | 3 | B. | -3 | C. | 1 | D. | -1或3 |
| A. | c2>b2>a2 | B. | c|b|>a|b| | C. | bc>ac | D. | ac>ab |
| A. | 0,1 | B. | 1,2 | C. | 0,1,2 | D. | 0,1,2,3 |