Question

【题目】在①，②，③这三个条件中任选一个，补充在下面问题中.已知：数列的前项和为，且，　 　.求：对大于1的自然数，是否存在大于2的自然数，使得，，成等比数列.若存在，求的最小值；若不存在，说明理由.

Answer 1

【答案】答案不唯一，见解析

【解析】

因为要使得,,成等比数列,不妨选择,分析可知数列是首项为1,公差为3的等差数列,进而得到,从而计算,再根据二次函数的最值分析的最小值即可.

由,,即,

可得数列是首项为1,公差为3的等差数列,

则,

假设对大于1的自然数,存在大于2的自然数,使得,,成等比数列,

可得,即,

两边平方可得,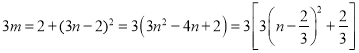

由在,且递增,可得时,取得最小值6,

可得此时取得最小值6,

故存在大于2的自然数,使得,,成等比数列,且的最小值为6.