题目内容
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,是否存在整数
时,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
【答案】(1)![]() (2)存在;
(2)存在;![]() 的最大值为-1
的最大值为-1
【解析】
(1)求得![]() ,根据题设条件,得到
,根据题设条件,得到![]() ,即可求解;
,即可求解;
(2)假设存在整数![]() ,使得不等式
,使得不等式![]() 恒成立,当
恒成立,当![]() 时,函数
时,函数![]() ,求得函数的导数,令
,求得函数的导数,令![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与最值,结合零点的存在定理和函数的最值,即可求解.
的单调性与最值,结合零点的存在定理和函数的最值,即可求解.
(1)由题意,函数![]() ,则
,则![]() ,
,
因为曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
所以![]() ,解得
,解得![]() .
.
(2)假设存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 恒成立,
恒成立,
当![]() 时,函数
时,函数![]() ,可得
,可得![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() 单调递增,且
单调递增,且![]() ,
,![]() ,
,
所以存在![]() 使得
使得![]() ,
,
因为当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() 单调递增,
单调递增,
所以![]() 时,
时,![]() 取得极小值,也是最小值,
取得极小值,也是最小值,
此时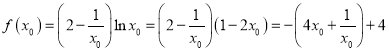 ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]() ,且
,且![]() 为整数,所以
为整数,所以![]() ,即
,即![]() 的最大值为-1.
的最大值为-1.

【题目】某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)请估计该市公众对“车辆限行”的赞成率和被调查者的年龄平均值;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记被选4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若在这50名被调查者中随机发出20份的调查问卷,记![]() 为所发到的20人中赞成“车辆限行”的人数,求使概率
为所发到的20人中赞成“车辆限行”的人数,求使概率![]() 取得最大值的整数
取得最大值的整数![]() .
.
【题目】某公司A产品生产的投入成本x(单位:万元)与产品销售收入y(单位:十万元)存在较好的线性关系,下表记录了该公司最近8次该产品的相关数据,且根据这8组数据计算得到y关于x的线性回归方程为![]() .
.
x(万元) | 6 | 7 | 8 | 11 | 12 | 14 | 17 | 21 |
y(十万元) | 1.2 | 1.5 | 1.7 | 2 | 2.2 | 2.4 | 2.6 | 2.9 |
(1)求![]() 的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
(2)该公司B产品生产的投入成本u(单位:万元)与产品销售收入v(单位:十万元)也存在较好的线性关系,且v关于u的线性回归方程为![]() .
.
(i)估计该公司B产品投入成本30万元后的毛利率(毛利率![]() );
);
(ii)判断该公司A,B两个产品都投入成本30万元后,哪个产品的毛利率更大.
【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销.定价为1000元/件.试销结束后统计得到该4S店这30天内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 | 6 | 3 |
(1)若该4S店试销期间每个零件的进价为650元/件,求试销连续30天中该零件日销售总利润不低于24500元的频率;
(2)试销结束后,这款零件正式上市,每个定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有60件,批发价为550元/件;小箱每箱有45件,批发价为600元/件.该4S店决定每天批发两箱,根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店.假设该4店试销后的连续30天的日销售量(单位:件)的数据如下表:
日销售量 | 50 | 70 | 90 | 110 |
频数 | 5 | 15 | 8 | 2 |
(ⅰ)设该4S店试销结束后连续30天每天批发两大箱,这30天这款零件的总利润;
(ⅱ)以总利润作为决策依据,该4S店试销结束后连续30天每天应该批发两大箱还是两小箱?