题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性:
的单调性:
(2)若函数![]() 在区间
在区间![]() 上的最小值为0,求
上的最小值为0,求![]() 的值.
的值.
【答案】(1)见解析(2)![]()
【解析】
(1)求导,根据导数讨论参数![]() ,再由参数讨论单调性;
,再由参数讨论单调性;
(2)由(1)的讨论可知当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.然后比较
上单调递增.然后比较![]() 与1的大小,若
与1的大小,若![]() ,则其最小值为
,则其最小值为![]() ,若
,若![]() ,其最小值为
,其最小值为![]() ,分别求出
,分别求出
![]() 后,看是否满足条件,可求出
后,看是否满足条件,可求出![]() 的值.
的值.
(1)因为![]() ,所以
,所以![]() ,
,
①当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)当![]() 时,函数
时,函数![]() ,不符合题意
,不符合题意
当![]() 时,由(1)可知
时,由(1)可知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
①当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() 的最小值为
的最小值为![]() ,由题得
,由题得![]() ,解得
,解得![]() ,符合题意.
,符合题意.
②当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,所以
上单调递增,所以![]() 的最小值为
的最小值为![]() .
.
由题得![]() ,解得
,解得![]() ,不符合题意.
,不符合题意.
综上所述,![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
【题目】如图,四棱锥O﹣ABCD的底面是边长为1的菱形,OA=2,∠ABC=60°,OA⊥平面ABCD,M、N分别是OA、BC的中点.
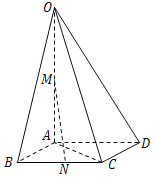
(1)求证:直线MN∥平面OCD;
(2)求点M到平面OCD的距离.