题目内容
已知数列 的前n项和为
的前n项和为 ,且
,且 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 令
 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前n项和为
的前n项和为 ,且
,且 .
.(1) 求数列
 的通项公式;
的通项公式;(2) 令

 ,求数列
,求数列 的前
的前 项和
项和 .
.(1)  (2)
(2)
 (2)
(2)
本试题主要是考查而来通项公式与前n项和之间的关系式,然后利用错误相减法求解数列的和的综合运用。
(1)首先分析当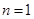 时,
时,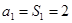
当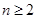 时,
时,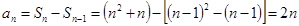 ,综合可知结论。
,综合可知结论。
(2)由已知: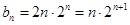
那么根据通项公式的特点可以求解数列的前n项和。
解:(1)当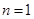 时,
时,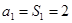 .................2分
.................2分
当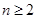 时,
时,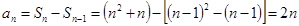
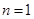 时,也适合上式。
时,也适合上式。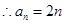 ...........................6分
...........................6分
(2)由已知: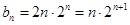
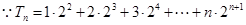 ①
①
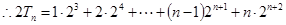 ②..................8分
②..................8分
①-②得 .............................12分
.............................12分
(1)首先分析当
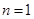 时,
时,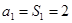
当
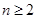 时,
时,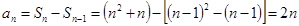 ,综合可知结论。
,综合可知结论。(2)由已知:
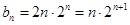
那么根据通项公式的特点可以求解数列的前n项和。
解:(1)当
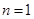 时,
时,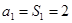 .................2分
.................2分当
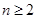 时,
时,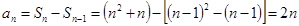
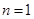 时,也适合上式。
时,也适合上式。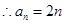 ...........................6分
...........................6分 (2)由已知:
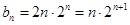
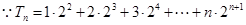 ①
①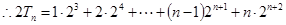 ②..................8分
②..................8分①-②得
 .............................12分
.............................12分 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
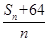 的最小值;
的最小值;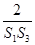 +
+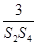 +…+
+…+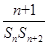 <
<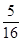 ;
;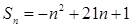 ,
,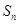 的最大值,并求出相应的
的最大值,并求出相应的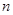 的值.
的值.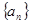 的前
的前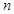 项和为
项和为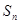 ,且
,且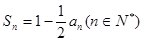
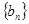 的通项公式
的通项公式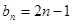 ,记
,记 ,求数列
,求数列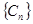 的前
的前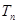 .
. 和等比数列
和等比数列 中,a1=2b1=2,b6=32,
中,a1=2b1=2,b6=32,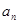 和
和 ;
;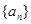 的前
的前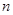 项和为
项和为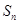 ,已知
,已知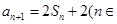 N
N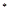 ).
).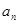 与
与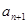 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为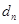 的等差数列,求数列
的等差数列,求数列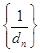 的前
的前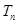 .(6分)
.(6分)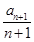 =
=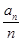 +
+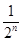 .
.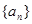 满足:
满足: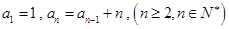 .
.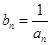 ,求数列
,求数列 的前
的前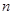 项和
项和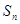 .
.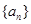 中,已知公差
中,已知公差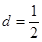 ,且
,且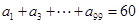 ,则
,则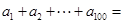 ( )
( )