题目内容
已知数列{an}的前n项和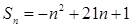 ,
,
(1)求数列{an}的通项公式;
(2)求前n项和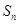 的最大值,并求出相应的
的最大值,并求出相应的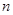 的值.
的值.
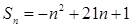 ,
,(1)求数列{an}的通项公式;
(2)求前n项和
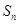 的最大值,并求出相应的
的最大值,并求出相应的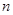 的值.
的值.(1)  ;
;
(2)
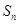 最得最大值,且最大值为
最得最大值,且最大值为
 ;
;(2)

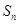 最得最大值,且最大值为
最得最大值,且最大值为
(1)根据 ,要注意验证当n=1时是否满足
,要注意验证当n=1时是否满足 得到的式子,不满足要写成分段函数的形式.
得到的式子,不满足要写成分段函数的形式.
(2)利用二次函数的性质,求出对称轴为 ,
, ,
, Sn取得最大值.
Sn取得最大值.
(1) 当 时,
时,
当 时,
时,

当 时不满足上式
时不满足上式


(2)

又

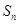 最得最大值,且最大值为
最得最大值,且最大值为
 ,要注意验证当n=1时是否满足
,要注意验证当n=1时是否满足 得到的式子,不满足要写成分段函数的形式.
得到的式子,不满足要写成分段函数的形式.(2)利用二次函数的性质,求出对称轴为
 ,
, ,
, Sn取得最大值.
Sn取得最大值.(1) 当
 时,
时,
当
 时,
时,
当
 时不满足上式
时不满足上式

(2)

又


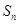 最得最大值,且最大值为
最得最大值,且最大值为

练习册系列答案
相关题目
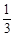 ,a2+a5=4,an=33,则n的值为( ).
,a2+a5=4,an=33,则n的值为( ).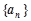 中,
中,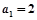 ,
,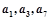 成等比数列,数列
成等比数列,数列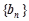 的前n项和为
的前n项和为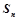 ,且
,且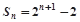 .
.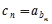 ,求数列
,求数列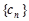 的前
的前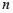 和
和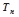 .
.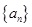 的前5项的和为30,前10项的和为100,则它的前15的和为( )
的前5项的和为30,前10项的和为100,则它的前15的和为( )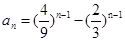 ,则数列{an}
,则数列{an}  的前n项和为
的前n项和为 ,且
,且 .
.
 ,求数列
,求数列 的前
的前 项和
项和 .
.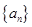 中,
中,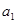 =1,当
=1,当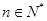 ,
,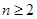 时,
时,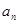 =
=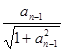 ,则数列
,则数列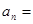 __________
__________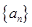 的前
的前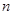 项和为
项和为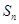 ,若
,若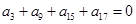 ,则
,则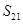 的值是( )
的值是( )

