题目内容
(12分)设等比数列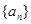 的前
的前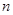 项和为
项和为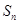 ,已知
,已知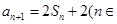 N
N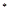 ).
).
(1)求数列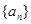 的通项公式;(6分)
的通项公式;(6分)
(2)在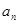 与
与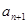 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为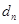 的等差数列,求数列
的等差数列,求数列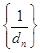 的前
的前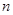 项和
项和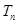 .(6分)
.(6分)
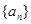 的前
的前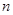 项和为
项和为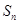 ,已知
,已知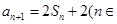 N
N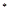 ).
).(1)求数列
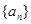 的通项公式;(6分)
的通项公式;(6分)(2)在
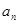 与
与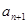 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为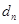 的等差数列,求数列
的等差数列,求数列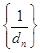 的前
的前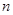 项和
项和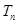 .(6分)
.(6分)(1)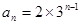 ;(2)
;(2)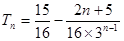 。
。
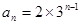 ;(2)
;(2)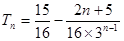 。
。(1)由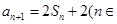 Z*),得
Z*),得 Z*,
Z*,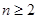 ),
),
再两式相减得: ,从而可得
,从而可得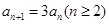 ,又因为
,又因为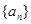 是等比数列,所以
是等比数列,所以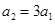 ,从而求出首项a1,得到
,从而求出首项a1,得到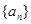 的通项公式.
的通项公式.
(2) 由(1)知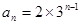 ,则
,则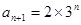 ,又∵
,又∵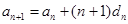 ,从而可得
,从而可得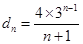 ,所以
,所以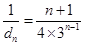 ,所以采用错位相减的方法求和即可.
,所以采用错位相减的方法求和即可.
(1)由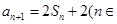 Z*)
Z*)
得 Z*,
Z*,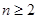 ),………………………………2分
),………………………………2分
两式相减得: ,
,
即 Z*,
Z*,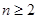 ),………………………………4分
),………………………………4分
∵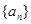 是等比数列,所以
是等比数列,所以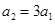 ; 又
; 又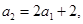 则
则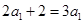 ,∴
,∴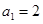 ,
,
∴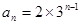 …………………………6分
…………………………6分
(2)由(1)知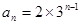 ,则
,则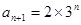
∵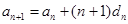 ,
,
∴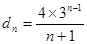 …………………8分
…………………8分
∵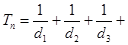 …
…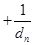
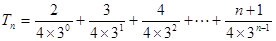 ①
①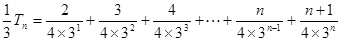 ②…………………10分
②…………………10分
①-②得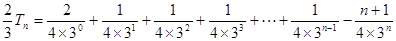
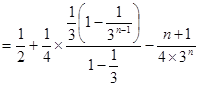
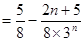 ……………………………………11分
……………………………………11分
∴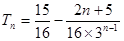 ……………………………………12分
……………………………………12分
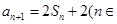 Z*),得
Z*),得 Z*,
Z*,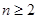 ),
),再两式相减得:
 ,从而可得
,从而可得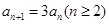 ,又因为
,又因为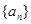 是等比数列,所以
是等比数列,所以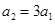 ,从而求出首项a1,得到
,从而求出首项a1,得到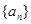 的通项公式.
的通项公式.(2) 由(1)知
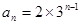 ,则
,则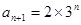 ,又∵
,又∵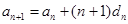 ,从而可得
,从而可得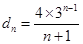 ,所以
,所以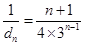 ,所以采用错位相减的方法求和即可.
,所以采用错位相减的方法求和即可.(1)由
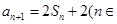 Z*)
Z*)得
 Z*,
Z*,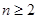 ),………………………………2分
),………………………………2分两式相减得:
 ,
, 即
 Z*,
Z*,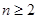 ),………………………………4分
),………………………………4分∵
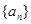 是等比数列,所以
是等比数列,所以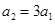 ; 又
; 又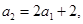 则
则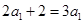 ,∴
,∴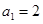 ,
,∴
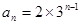 …………………………6分
…………………………6分(2)由(1)知
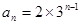 ,则
,则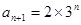
∵
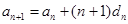 ,
,∴
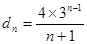 …………………8分
…………………8分∵
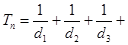 …
…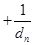
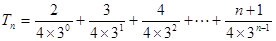 ①
①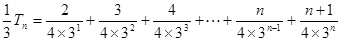 ②…………………10分
②…………………10分①-②得
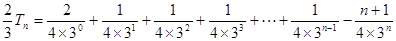
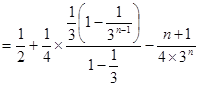
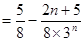 ……………………………………11分
……………………………………11分∴
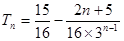 ……………………………………12分
……………………………………12分
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
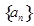 的前
的前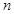 项和为
项和为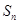 ,且
,且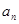 是
是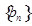 中,
中,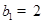 ,点
,点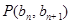 在直线
在直线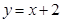 上.
上.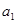 和
和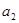 的值;
的值;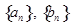 的通项
的通项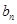 ;
;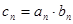 ,求数列
,求数列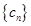 的前n项和
的前n项和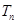 .
.  的前n项和为
的前n项和为 ,且
,且 .
.
 ,求数列
,求数列 的前
的前 项和
项和 .
.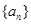 为等差数列,且
为等差数列,且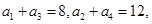
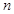 项和为
项和为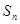 ,若
,若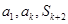 成等比数列,求正整数
成等比数列,求正整数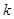 的值。
的值。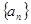 满足:
满足: .
. ,求数列
,求数列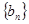 的前n项和
的前n项和 .
.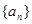 中各项均为正数,
中各项均为正数,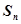 是数列
是数列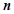 项和,且
项和,且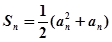 .
.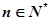 ,试比较
,试比较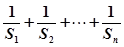 与
与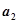 的大小.
的大小. 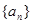 中,若
中,若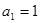 ,
,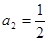 ,
,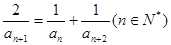 ,则该数列的通项为 .
,则该数列的通项为 . 
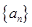 的前
的前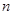 项和为
项和为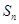 ,若
,若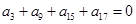 ,则
,则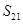 的值是( )
的值是( )


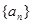 中,
中,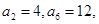 则公差d= ( )
则公差d= ( )