题目内容
10.关于x的方程x3+ax2+bx+c=0的三个实数根可作为一个椭圆、一个双曲线、一个抛物线的离心率,则$\frac{b-1}{a+1}$的取值范围是 ( )| A. | (-2,0) | B. | (0,2) | C. | (-1,0) | D. | (0,1) |
分析 依题意可知方程有一个根是1,进而可设x3+ax2+bx+c=0=(x-1)(x2+mx+n)根据多项式恒等的充要条件,的方程组,联立后可求得m和n,进而可构造函数f(x)=x2+mx+n,则可知f(x)=0的两个根x1,x2分别作为椭圆和双曲线的离心率,根据判别式大于0,令a为横轴,b为纵轴,建立平面直角坐标系,作出这三个不等式所对应的平面区域S,设P(a,b)是平面区域S内的任意一点,A(-1,1),则可知$\frac{b-1}{a+1}$的几何意义是直线的斜率,进而可求得范围.
解答 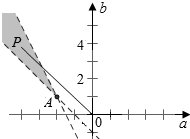 解:依题意,关于x的方程 x3+ax2+bx+c=0有一个根是1
解:依题意,关于x的方程 x3+ax2+bx+c=0有一个根是1
所以可设x3+ax2+bx+c=0=(x-1)(x2+mx+n)
根据多项式恒等的充要条件,得
m-1=a①
n-m=b②
n+c=0③
取①②两式联立得
m=a+1,n=a+b+1
构造函数 f(x)=x2+mx+n 即 f(x)=x2+(a+1)x+(a+b+1)
依题意f(x)=0的两个根x1,x2分别作为椭圆和双曲线的离心率
故 0<x1<1<x2
根据一元二次方程根的分布,可得关于实系数a,b的约束条件:
判别式=(a+1)2-4(a+b+1)=(a-1)2-4b-4>0
f(0)=a+b+1>0,f(1)=2a+b+3<0
令a为横轴,b为纵轴,建立平面直角坐标系,作出这三个不等式所对应的平面区域S,
设P(a,b)是平面区域S内的任意一点,A(-1,1),k=$\frac{b-1}{a+1}$,则k的几何意义是直线PA的斜率.
作图,得-2<k<0
故选:A.
点评 本题主要考查了圆锥曲线的综合知识.涉及到了方程的根的分布,多项式恒等等知识,属中档题.

练习册系列答案
相关题目
20.“$\sqrt{x}$>0”是“x>0”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
15.设a=log32,b=ln2,c=5${\;}^{\frac{1}{2}}$,则a、b、c三个数的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
2.设x>0,则方程x+$\frac{1}{x}$=2sinx的根的情况是( )
| A. | 有实根 | B. | 无实根 | C. | 恰有一实根 | D. | 无法确定 |
