题目内容
19.锐角三角形ABC中,$S=\frac{{c}^{2}-({a}^{2}-{b}^{2})}{4k}$,c既不为最大边也不为最小边,则k的取值范围是($\sqrt{2}$-1,1).分析 先根据余弦定理和面积公式表示出$S=\frac{{{c^2}-{{(a-b)}^2}}}{4k}$,得到关于C的关系式,再由万能公式和角C的范围确定答案.
解答 解:∵c既不为最大边也不为最小边,
∴C既不是△ABC的最大角也不是△ABC的最小角,
∵c2=a2+b2-2abcosC,
∴$S=\frac{{{c^2}-{{(a-b)}^2}}}{4k}$=$\frac{{c}^{2}-{a}^{2}-{b}^{2}+2ab}{4k}$=$\frac{2ab-2abcosC}{4k}$=$\frac{ab(1-cosC)}{2k}$,
又S=$\frac{1}{2}$absinC,
∴sinC=$\frac{1-cosC}{k}$,
则k=$\frac{1-cosC}{sinC}$=$\frac{1-(1-2si{n}^{2}\frac{C}{2})}{2sin\frac{C}{2}cos\frac{C}{2}}$=$\frac{2si{n}^{2}\frac{C}{2}}{2sin\frac{C}{2}cos\frac{C}{2}}$=tan$\frac{C}{2}$,
∵锐角三角形ABC中C既不是△ABC的最大角也不是△ABC的最小角,
∴45°<C<90°,$\frac{45°}{2}$<$\frac{C}{2}$<45°
∴$\sqrt{2}$-1<tan$\frac{C}{2}$<1,
∴$\sqrt{2}$-1<k<1
故答案为:($\sqrt{2}$-1,1)
点评 本题主要考查余弦定理和三角形面积公式的应用,利用正弦定理和余弦定理结合三角函数的倍角公式是解决本题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
10.关于x的方程x3+ax2+bx+c=0的三个实数根可作为一个椭圆、一个双曲线、一个抛物线的离心率,则$\frac{b-1}{a+1}$的取值范围是 ( )
| A. | (-2,0) | B. | (0,2) | C. | (-1,0) | D. | (0,1) |
7.集合M={x|x=k•90°+45°,k∈Z},N={x|x=k•45°+90°,k∈Z},则有( )
| A. | M=N | B. | N?M | C. | M?N | D. | M∩N=∅ |
14.集合M={m|m=2n-1,n∈N*,m<60}的元素个数是( )
| A. | 59 | B. | 31 | C. | 30 | D. | 29 |
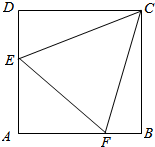 在边长为1的正方形ABCD中,E,F分别为AD,AB边上的点,△AEF的
在边长为1的正方形ABCD中,E,F分别为AD,AB边上的点,△AEF的