题目内容
7.满足条件|z-i|=|1+$\sqrt{3}$i|的复数z在复平面上对应的点(x,y)的轨迹为( )| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |
分析 根据复数的几何意义进行求解即可.
解答 解:由|z-i|=|1+$\sqrt{3}$i|得|z-i|=|1+$\sqrt{3}$i|=2,
即z的几何意义是到定点(0,1)的距离等于2,
即复数z在复平面上对应的点(x,y)的轨迹为是以定点(0,1)为圆心,2为半径的圆,
故选:C.
点评 本题主要考查复数的几何意义,利用复数的模长进行求解是解决本题的关键.

练习册系列答案
相关题目
19.下列四组函数中,表示同一函数的是( )
| A. | y=$\sqrt{{x}^{2}}$与y=x | B. | y=x0与y=1 | ||
| C. | y=2${\;}^{lo{g}_{4}x}$与y=$\frac{x}{\sqrt{x}}$ | D. | y=x与y=($\sqrt{x})^{2}$2 |
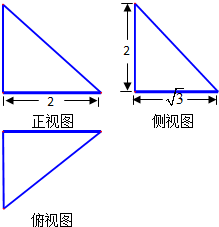 三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{{2\sqrt{3}}}{3}$.
三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{{2\sqrt{3}}}{3}$.