题目内容
【题目】平面直角坐标系中,圆![]() 方程为
方程为![]() ,点
,点![]() ,直线
,直线![]() 过点
过点![]()
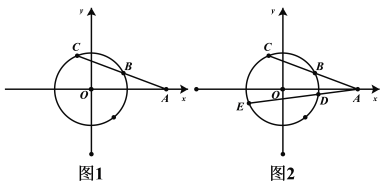
(1)如图1,直线的斜率为![]() ,直线
,直线![]() 交圆
交圆![]() 于
于![]() 不同两点,求弦
不同两点,求弦![]() 的长度;
的长度;
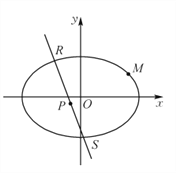
(2)动点![]() 在圆
在圆![]() 上作圆周运动,线段
上作圆周运动,线段![]() 的中点为点
的中点为点![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(3)在(1)中,如图2,过点![]() 作直线
作直线![]() ,交圆
,交圆![]() 于
于![]() 不同两点,证明:
不同两点,证明:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)求出直线![]() 的方程,再求出圆心到直线的距离,利用垂径定理可求弦
的方程,再求出圆心到直线的距离,利用垂径定理可求弦![]() 的长.
的长.
(2)利用动点转移法可求![]() 的轨迹方程.
的轨迹方程.
(3)设直线![]() 的方程为:
的方程为:![]() ,联立直线
,联立直线![]() 的方程和圆的方程,消元后利用韦达定理可证
的方程和圆的方程,消元后利用韦达定理可证![]() 对任意的
对任意的![]() 总成立,从而可证
总成立,从而可证![]() .
.
(1)直线![]() 的方程为
的方程为![]() 即
即![]() ,
,
圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,故
,故 .
.
(2)设![]() ,则
,则![]() ,
,
故![]() ,所以点
,所以点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(3)我们证明:![]() 为定值.
为定值.
直线![]() 的斜率必存在.
的斜率必存在.
设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,
则![]() .
.
由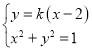 可得
可得![]() ,
,
故![]() ,
,![]() 即
即![]() .
.
所以![]()
![]() ,
,
故![]() 对任意的
对任意的![]() 总成立,又
总成立,又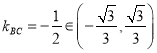 ,
,
所以![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目