题目内容
【题目】定义向量![]() 的“相伴函数”为
的“相伴函数”为![]() ,函数
,函数![]() 的“相伴向量”为
的“相伴向量”为![]() ,其中O为坐标原点,记平面内所有向量的“相伴函数”构成的集合为S.
,其中O为坐标原点,记平面内所有向量的“相伴函数”构成的集合为S.
(1)设![]() ,求证:
,求证:![]() ;
;
(2)已知![]() 且
且![]() ,求其“相伴向量”的模;
,求其“相伴向量”的模;
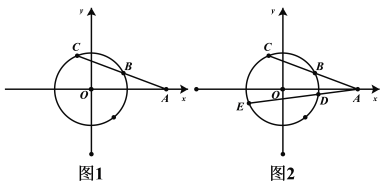
(3)已知![]()
![]() 为圆
为圆![]() 上一点,向量
上一点,向量![]() 的“相伴函数”
的“相伴函数”![]() 在
在![]() 处取得最大值,当点M在圆C上运动时,求
处取得最大值,当点M在圆C上运动时,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)把![]() 化为
化为![]() 形式,由定义证明;
形式,由定义证明;
(2)把![]() 化为
化为![]() 形式,得其“相伴向量”,由模公式可求模;
形式,得其“相伴向量”,由模公式可求模;
(3)先根据定义得到函数![]() 取得最大值时对应的自变量
取得最大值时对应的自变量![]() ,再结合几何意义求出
,再结合几何意义求出![]() 的取值范围,由正切的二倍角公式及函数的单调性可得结论.
的取值范围,由正切的二倍角公式及函数的单调性可得结论.
(1)![]()
![]() ,其“相伴向量”为
,其“相伴向量”为![]() ,
,
∴![]() ;
;
(2)![]()
![]()
![]() ,
,
其“相伴向量”为![]() ,
,
∴![]() ;
;
(3)向量![]() 的“相伴函数”为
的“相伴函数”为![]()
![]() ,其中
,其中![]() ,
,
当![]() 时,
时,![]() 取得最大值,故
取得最大值,故![]() ,∴
,∴![]() ,
,
∴ ,
,![]() 表示直线
表示直线![]() 的斜率,由几何意义知
的斜率,由几何意义知![]() ,令
,令![]() ,则
,则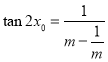 ,
,![]() ,
,
当![]() 时,
时,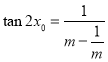 单调递减,∴
单调递减,∴![]() ,当
,当![]() 时,
时,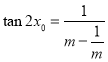 单调递减,∴
单调递减,∴![]() ,
,
综上所述,![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值