��Ŀ����
9���Ѻ���f��x��=sin2x��ͼ�������е�����ƽ���ƶ�$\frac{��}{6}$����λ���Ⱥõ�����y=g��x����ͼ�����й���y=g��x����˵����ȷ���ǣ�������| A�� | y=g��x����ͼ����ڵ㣨-$\frac{��}{3}$��0�����ĶԳ� | B�� | y=g��x����ͼ�����x=-$\frac{��}{6}$��Գ� | ||
| C�� | y=g��x��������[-$\frac{5��}{12}$��-$\frac{��}{6}$]�������� | D�� | y=g��x����[-$\frac{��}{6}$��$\frac{��}{3}$]�����ݼ� |
���� ����ƽ��֪ʶд������y=g��x���Ľ���ʽ���ж�
��1��x=-$\frac{��}{3}$ʱ��y=g��x����0�����������
��2��x=-$\frac{��}{6}$ʱ��y=g��x���١�1�������⣨2������
��3��x��[-$\frac{5��}{12}$��-$\frac{��}{6}$]ʱ��y=g��x�����������������⣨3����ȷ��
��4��x��[-$\frac{��}{6}$��$\frac{��}{3}$]ʱ��y=g��x������������ĺ����������⣨4������
��� �⣺�ߺ���f��x��=sin2x����ƽ��$\frac{��}{6}$����λ���õ�����y=g��x��=sin2��x+$\frac{��}{6}$��=sin��2x+$\frac{��}{3}$����
�ࣨ1����x=-$\frac{��}{3}$ʱ��y=g��x��=sin��-$\frac{2��}{3}$+$\frac{��}{3}$��=-$\frac{\sqrt{3}}{2}$��0��
�����⣨1������
��2����x=-$\frac{��}{6}$ʱ��y=g��x��=sin��-$\frac{��}{3}$+$\frac{��}{3}$��=0�١�1�������⣨2������
��3����x��[-$\frac{5��}{12}$��-$\frac{��}{6}$]ʱ��2x+$\frac{��}{3}$��[-$\frac{��}{2}$��0]��
�ຯ��y=g��x��=sin��-$\frac{2��}{3}$+$\frac{��}{3}$�����������������⣨3����ȷ��
��4����x��[-$\frac{��}{6}$��$\frac{��}{3}$]ʱ��2x+$\frac{��}{3}$��[0����]��
�ຯ��y=g��x��=sin��-$\frac{2��}{3}$+$\frac{��}{3}$������������ĺ����������⣨4������
��ѡ��C��
���� ���⿼�������Ǻ���ͼ��ƽ�Ƶ�֪ʶ������ʱӦͨ��ͼ��ƽ�Ƶõ������Ľ���ʽ���ٸ��ݽ���ʽ�ж������Ƿ�����ѡ���е��������ɣ����ڻ����⣮

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�| A�� | [-2��-1] | B�� | [-1��6�� | C�� | [-1��3] | D�� | [-2��6�� |
| A�� | 8��0.2 | B�� | 4��0.4 | C�� | 5��0.32 | D�� | 7��0.45 |
| A�� | 5 | B�� | $\frac{9}{2}$ | C�� | $\frac{1}{12}$ | D�� | 17 |
| A�� | ��$\sqrt{5}$��$\sqrt{10}$] | B�� | ��1��$\sqrt{10}$] | C�� | ��1��$\sqrt{5}$] | D�� | [$\sqrt{5}$��+�ޣ� |
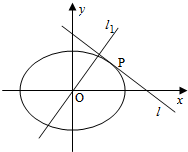 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$��a��b��0����������Ϊ$\frac{1}{2}$��˳���������ĸ����㹹�ɵ��ı��ε����Ϊ4$\sqrt{3}$��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$��a��b��0����������Ϊ$\frac{1}{2}$��˳���������ĸ����㹹�ɵ��ı��ε����Ϊ4$\sqrt{3}$��