题目内容
8.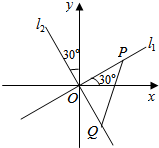 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.(Ⅰ)若x=$\frac{2\sqrt{3}}{3}$x1,y=$\sqrt{3}$x2,求动点M(x,y)的轨迹C的方程;
(Ⅱ)过(-1,0)的直线l与(Ⅰ)中的轨迹C交于不同的两点A、B,若△AOB的面积为$\frac{6\sqrt{2}}{7}$,求圆心在原点O且与直线l相切的圆的方程.
分析 (Ⅰ)通过将点P、Q分别代入l1、l2,利用已知条件计算即可;
(Ⅱ)当直线l垂直于x轴时,易得S△AOB=$\frac{3}{2}$,不符合题意;当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),k≠0,并与椭圆方程联立,利用韦达定理、点到直线的距离计算即可.
解答 解:(Ⅰ)根据题意可得:l1:y=$\frac{\sqrt{3}}{3}$x,l2:y=-$\sqrt{3}$x,
∵点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,
∴y1=$\frac{\sqrt{3}}{3}$x1,y2=-$\sqrt{3}$x2,
又由已知得:l1⊥l2,且|PQ|=2,
∴(x12+y12)+(x22+y22)=4,化简得:$\frac{{{x}_{1}}^{2}}{3}+$x22=1,
由x=$\frac{2\sqrt{3}}{3}$x1 ,y=$\sqrt{3}$x2,可得x1=$\frac{\sqrt{3}}{2}$x,x2=$\frac{\sqrt{3}}{3}$y,
∴动点M(x,y)的轨迹C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1;
(Ⅱ)当直线l垂直于x轴时,得A(-1,$\frac{3}{2}$)、B(-1,-$\frac{3}{2}$),
此时S△AOB=$\frac{1}{2}$•|AB|•|OF1|=$\frac{1}{2}$×3×1=$\frac{3}{2}$,不符合题意.
当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),k≠0,
代入椭圆方程,消去y得:(3+4k2)x2+8k2x+4k2-12=0.
显然△>0成立,设A(x1,y1)、B(x2,y2),
则x1+x2=-$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1•x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$.
又|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$
又圆O的半径r=$\frac{|k|}{\sqrt{1+{k}^{2}}}$,
所以S△AOB=$\frac{1}{2}$•|AB|•r=$\frac{1}{2}$•$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$•$\frac{|k|}{\sqrt{1+{k}^{2}}}$=$\frac{6\sqrt{2}}{7}$.
化简得17k4+k2-18=0,即(k2-1)(17k2+18)=0,
解得k12=1,k22=-$\frac{18}{17}$(舍),∴r=$\frac{|k|}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{2}}{2}$,
故圆O的方程为:x2+y2=$\frac{1}{2}$.
点评 本题是一道直线与圆锥曲线的综合题,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于中档题.

 已知过抛物线y2=2px(p>0)上一点A(4,y0)到焦点F的距离为5.
已知过抛物线y2=2px(p>0)上一点A(4,y0)到焦点F的距离为5.