题目内容
18.已知命题p:a2<a(a∈R),命题q:对任意x∈R,都有x2+4ax+1≥0(a∈R)(1)若命题p且q为假,p或q为真,求实数a的取值范围;
(2)若命题p,q为真时,实数a的取值集合分别为集合M和集合N,则“x∈M或x∈N”是“x∈(M∩N)”的什么条件?并说明理由(提示:充分不必要条件,必要不充分条件,充要条件,既不充分又不必要条件)
分析 (1)分别求出p,q分别为真,假命题时的a的范围,取交集,从而求出a的范围;(2)求出集合M、N和M∩N,从而判断出结论.
解答 解:(1)∵命题p:a2<a,解得;0<a<1,若p假:则a≤0或a≥1,
命题q:对任何x∈R,都有x2+4ax+1≥0,解得:-$\frac{1}{2}$≤a≤$\frac{1}{2}$,若q假,则a<-$\frac{1}{2}$或a>$\frac{1}{2}$,
∵命题p与命题q中有且只有一个成立,
0<a<1; a<-$\frac{1}{2}$或a>$\frac{1}{2}$,取二者交集$\frac{1}{2}$<a<1,
a≤0或a≥1;-$\frac{1}{2}$≤a≤$\frac{1}{2}$,取二者交集-$\frac{1}{2}$≤a≤0,
∴实数a的取值范围:$\frac{1}{2}$<a<1,或-$\frac{1}{2}$≤a≤0;
(2)命题p为真时:0<a<1,
∴M={a|0<a<1};
命题q为真时:-$\frac{1}{2}$≤a≤$\frac{1}{2}$,
∴N={a|-$\frac{1}{2}$≤a≤$\frac{1}{2}$},
∴M∩N={a|0<a≤$\frac{1}{2}$};
∴x∈M或x∈N”是“x∈(M∩N)”的必要不充分条件.
点评 本题考查了复合命题的判断,考查二次函数的性质,是一道中档题.

练习册系列答案
相关题目
7.若函数f(x)在区间[-4,4]上为偶函数且在区间[0,4]上单调递增,则下列不等式成立的是( )
| A. | f(-3)<f(-2) | B. | f(3)<f(2) | C. | f(-3)<f(-π) | D. | f(-2)<f(1) |
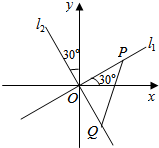 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.