题目内容
13.在△ABC中,2acosB=c,试判断△ABC的形状.分析 由正弦定理可得 sin(A+B)=2sinAcosB,由两角和的正弦公式可求得 sin(A-B)=0,根据-π<A-B<π,故A-B=0,从而得到△ABC的形状为等腰三角形.
解答 解:∵2acosB=c,
∴由正弦定理可得 sin(A+B)=2sinAcosB,
由两角和的正弦公式可得 sinAcosB+cosAsinB=2sinAcosB,
∴sin(A-B)=0,又-π<A-B<π,
∴A-B=0,
故△ABC的形状为等腰三角形.
点评 本题考查正弦定理的应用,已知三角函数值求角的大小,得到 sin(A-B)=0,是解题的关键.

练习册系列答案
相关题目
5.在△ABC中,内角A,B,C所对边长分别为a,b,c,若c=2$\sqrt{3}$,B=$\frac{π}{4}$,C=$\frac{π}{3}$,则a等于( )
| A. | $\sqrt{3}+\sqrt{2}$ | B. | $\sqrt{2}+\sqrt{6}$ | C. | $\sqrt{3}+\sqrt{6}$ | D. | 2+$\sqrt{3}$ |
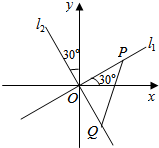 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.