题目内容
16.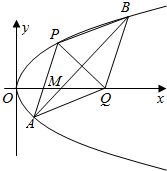 已知过抛物线y2=2px(p>0)上一点A(4,y0)到焦点F的距离为5.
已知过抛物线y2=2px(p>0)上一点A(4,y0)到焦点F的距离为5.(1)求p、y0的值;
(2)设点M(m,0)(m为常数),是否存在过M的直线(与x轴不垂直)与抛物线交于A、B两点,AB的垂直平分线与抛物线和x轴分别交于P、B两点,AB的垂直平分线与抛物线和x轴分别交于P、Q(P、Q位于直线两侧),使四边形APBQ为一内角是$\frac{π}{3}$的菱形,若存在,求直线方程;若不存在,请说明理由.
分析 (1)求出抛物线的准线,由抛物线的定义,可得p=2,将A代入抛物线方程,可得y0的值;
(2)设出直线AB的方程,代入抛物线方程,运用韦达定理和弦长公式,中点坐标公式,可得AB的中点,即为PQ的中点,设出PQ的方程,求得P,Q的坐标,由四边形APBQ为一内角是$\frac{π}{3}$的菱形,可得|AB|=$\sqrt{3}$|PQ|,解方程可得m=2,即可判断是否存在.
解答 解:(1)抛物线y2=2px的准线为x=-$\frac{p}{2}$,
即有抛物线定义可得,|AF|=4+$\frac{P}{2}$=5,
解得p=2,
抛物线方程为y2=4x,
即有y02=16,可得y0=±4;
(2)设直线AB:y=k(x-m),
代入抛物线方程y2=4x,
可得k2x2-(2mk2+4)x+k2m2=0,
设A(x1,y1),B(x2,y2),
则有x1+x2=2m+$\frac{4}{{k}^{2}}$,x1x2=m2.
即有AB的中点C(m+$\frac{2}{{k}^{2}}$,$\frac{2}{k}$),
|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{(m+2-\frac{2}{{k}^{2}})^{2}-4{m}^{2}}$,
由题意可得直线PQ:y-$\frac{2}{k}$=-$\frac{1}{k}$(x-m-$\frac{2}{{k}^{2}}$),
令y=0可得x=m+2+$\frac{2}{{k}^{2}}$,
即有Q(m+2+$\frac{2}{{k}^{2}}$,0),
由C为PQ的中点,可得P(m+$\frac{2}{{k}^{2}}$-2,$\frac{4}{k}$),
代入抛物线方程可得k2=$\frac{2}{m-2}$,①
即有P($\frac{4}{{k}^{2}}$,$\frac{4}{k}$),
|PQ|=$\sqrt{{4}^{2}+\frac{16}{{k}^{2}}}$,
由四边形APBQ为一内角是$\frac{π}{3}$的菱形,可得
|AB|=$\sqrt{3}$|PQ|,
即有$\sqrt{1+{k}^{2}}$•$\sqrt{16-4{m}^{2}}$=$\sqrt{3}$•$\sqrt{16+8m-16}$,②
解得m=2(负值舍),k不存在.
故不存在这样的直线AB,使四边形APBQ为一内角是$\frac{π}{3}$的菱形.
点评 本题考查抛物线的定义和方程、性质的运用,考查直线方程和抛物线方程联立,运用韦达定理和弦长公式,及中点坐标公式,考查运算能力,属于中档题.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案| A. | f(-3)<f(-2) | B. | f(3)<f(2) | C. | f(-3)<f(-π) | D. | f(-2)<f(1) |
| A. | $\sqrt{3}+\sqrt{2}$ | B. | $\sqrt{2}+\sqrt{6}$ | C. | $\sqrt{3}+\sqrt{6}$ | D. | 2+$\sqrt{3}$ |
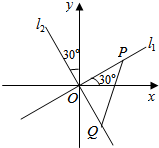 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.