题目内容
18.已知函数f(x)满足f(1)=$\frac{1}{2}$,f(n+1)=$\frac{1}{1+f(n)}$,求|f(n+1)-f(n)|的最大值.分析 由条件可得f(2),f(3),f(4),f(5),归纳特点,求出n=1,2,3,4,求出|f(n+1)-f(n)|的数值,总结变化情况,即可得到最大值.
解答 解:由f(1)=$\frac{1}{2}$,f(n+1)=$\frac{1}{1+f(n)}$,
可得f(2)=$\frac{2}{3}$,f(3)=$\frac{3}{5}$,f(4)=$\frac{5}{8}$,f(5)=$\frac{8}{13}$,…
以后的每一项的分子、分母均为前两项的和,
则|f(2)-f(1)|=|$\frac{2}{3}$-$\frac{1}{2}$|=$\frac{1}{6}$,|f(3)-f(2)|=$\frac{1}{15}$,
|f(4)-f(3)|=$\frac{1}{40}$,|f(5)-f(4)|=$\frac{1}{104}$,…,显然分母越来越大,
分子不变,则有最大值为$\frac{1}{6}$.
点评 本题考查数列相邻两项的差的绝对值的变化,考查数列的各项的变化特点,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
7.已知二项式(x+3y)n(n∈N+)的展开式的二项式系数之和为128,则展开式的各项系数之和为( )
| A. | 128 | B. | 64 | C. | 28 | D. | 214 |
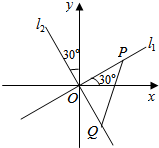 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.