题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}(a-1){x}^{2}-2ax+b+2,x≤0\\(a-1)x+b+2,x>0\end{array}\right.$,则以下命题中正确的是(1)(4)(把所有真命题的序号都填上)(1)若a=b=2,则不等式f(x)<9的解集为(-1,5);
(2)若a=b=2,则函数f(x)为单调函数;
(3)对任意实数a,b,函数f(x)均为单调函数;
(4)若不等式f(x)<0的解集为非空集合D,且D⊆(-1,2),则z=2a-b的取值范围为(4,+∞);
(5)若不等式f(x)<0的解集不可能为空集.
分析 将a=b=2代入,解不等式f(x)<9,可判断(1);
将a=b=2代入,分析函数f(x)的单调性,可判断(2),(3);
根据不等式的解集关系转化为不等式组,利用数形结合以及线性规划的知识进行求解即可得到结论,可判断(4);
举出反例,可判断(5).
解答 解:(1)若a=b=2,则f(x)=$\left\{\begin{array}{l}{x}^{2}-4x+4,x≤0\\ x+4,x>0\end{array}\right.$
当x≤0时,解f(x)=x2-4x+4<9得:x∈(-1,5);
∴x∈(-1,0],
当x>0时,解f(x)=x+4<9得:x∈(-∞,5);
∴x∈(0,5),
综上所述,不等式f(x)<9的解集为(-1,5),故(1)正确;
(2)若a=b=2,则f(x)=$\left\{\begin{array}{l}{x}^{2}-4x+4,x≤0\\ x+4,x>0\end{array}\right.$
当x≤0时,f(x)=x2-4x+4为减函数,
当x>0时,f(x)=x+4为增函数,
函数f(x)不为单调函数,故(2)(3)错误;
(4)∵不等式f(x)<0的解集为非空集合D,且D⊆(-1,2),
∴等价为$\left\{\begin{array}{l}a-1>0\\ f(-1)=3a+b+1≥0\\ f(0)=b+2≥0\\ f(2)=2a+b≥0\end{array}\right.$
由z=2a-b得b=2a-z,
作出不等式组对应的平面区域如图,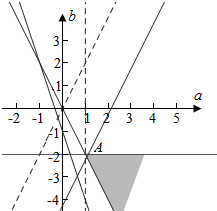
平移直线b=2a-z,由图象可知
当直线b=2a-z经过点A时,直线的截距最大,此时z最小,
由$\left\{\begin{array}{l}a-1=0\\ b+2=0\end{array}\right.$,解得 $\left\{\begin{array}{l}a=1\\ b=-2\end{array}\right.$,
即A(1,-2),
此时z=2a-b=2-(-2)=4,
故z∈(4,+∞),故(4)正确;
解当a=b=1时,f(x)=$\left\{\begin{array}{l}-2x+3,x≤0\\ 3,x>0\end{array}\right.$∈[3,+∞),
此时不等式f(x)<0的解集为空集,故(5)错误;
故正确的命题有:(1)(4),
故答案为:(1)(4)
点评 本题主要分段函数的应用,考查线性规划的应用,根据不等式的关系转化为不等式组,利用线性规划的知识以及数形结合是解决本题的关键.综合性较强,难度较大.

 名校课堂系列答案
名校课堂系列答案| A. | $\sqrt{3}+\sqrt{2}$ | B. | $\sqrt{2}+\sqrt{6}$ | C. | $\sqrt{3}+\sqrt{6}$ | D. | 2+$\sqrt{3}$ |
| A. | p(A|B)=P(B|A) | B. | P(A∩B|A)=P(B) | C. | $\frac{P(AB)}{P(B)}$=P(B|A) | D. | p(A|B)=$\frac{n(AB)}{n(B)}$ |
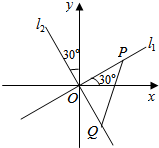 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.